Fuel, gas mixtures and heat capacity
In heat engines (machines), the working fluid is a mixture of various gases. If the components of the mixture do not enter into chemical reactions among themselves, and each component obeys the Klaiperon equation of state, then such a mixture is considered as an ideal gas.
To calculate the mixture, it is necessary to determine μ cm - the average molar mass and R c m - the specific gas constant of the mixture. To determine them, it is necessary to know the composition of the mixture, that is, which components and in what quantities form this mixture, what parameters each component included in the mixture has.
Each component of the mixture behaves as if there were no other gases in the mixture, occupies the entire available volume in which the mixture is located, follows its own equation of state and exerts its so-called partial pressure on the walls, while the temperature of all components of the mixture is the same and equal to mixture temperature.
According to Dalton's law, the pressure of the mixture P is equal to the sum of the partial pressures of the individual components included in the mixture:
where n is the number of mixture components.
According to Amag's law, the volume of the mixture V is equal to the sum of the partial volumes of the individual components included in the mixture at the temperature and pressure of the mixture:
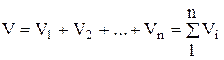 , (1.21)
, (1.21)
where - partial volume, m 3; V- volume of the mixture, m 3
The composition of the mixture is given by volume (molar) or mass fractions.
Volume fraction of the i-th component is the ratio of the partial volume of the component to the volume of the mixture, i.e., then the sum of the volume fractions of the components of the mixture is 1, i.e. . If the value is given in %, then their sum = 100%.
Molar fraction of the i-th component n i is the ratio of the number of kilomoles of the component N i to the number of kilomoles of the mixture N, i.e., where ![]() , , i.e. the number of kilomoles of each component and the mixture as a whole is equal to the ratio of the corresponding component and the mixture as a whole to the volume occupied by one kilomol.
, , i.e. the number of kilomoles of each component and the mixture as a whole is equal to the ratio of the corresponding component and the mixture as a whole to the volume occupied by one kilomol.
Considering that an ideal gas under the same conditions has the same volume of kilomole, then after substitution we get: , i.e. for ideal gases molar and volume fractions are numerically equal.
Mass fraction of the i-th component is the ratio of the mass of the component to the mass of the mixture: , it follows that the mass of the mixture is equal to the sum of the masses of the components, and also the sum of the mass fractions of the components is equal to 1 (or 100%).
Conversion of volume fractions to mass fractions and vice versa is based on the following ratios:
![]() ,
,
where ρ = μ / 22.4, kg / m 3.
Whence it follows that the mass fraction of the i-th component will be determined from the relation:
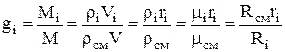 ,
,
where is the density of the mixture, kg / m 3, is the volume fraction of the i-th component.
In the future, it can be determined through volume fractions.
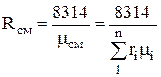 .
.
Density mixtures for volume fractions is determined from the ratio
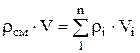 , where
, where 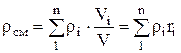 , (1.22)
, (1.22)
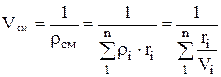 .
.
Partial pressure is determined by the formulas:
![]() or
or 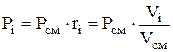 (1.23)
(1.23)
The equations of state of the components and the mixture as a whole have the form:
![]() ;
;
![]() ,
,
whence, after transformations, we obtain for massive shares
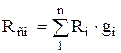 ,
, 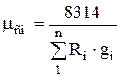 . (1.24)
. (1.24)
Density and specific volume of the mixture for massive share:
; 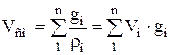 . (1.25)
. (1.25)
To calculate partial pressures, the formula is used:
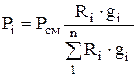 . (1.26)
. (1.26)
The conversion of mass fractions into volume fractions is carried out according to the formula:
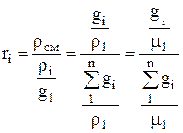 .
.
When determining the heat capacity of a mixture of gases, it is assumed that in order to heat (cool) a gas mixture, it is necessary to heat (cool) each of the components of the mixture
where Q i =M i c i ∆t is the heat spent on changing the temperature of the i-th component of the mixture, c i is the mass heat capacity of the i-th component of the mixture.
The heat capacity of the mixture is determined from the ratio (if the mixture is given by mass fractions)
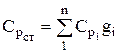 , similarly
, similarly 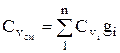 . (1.28)
. (1.28)
The molar and volumetric heat capacities for a mixture given by volume fractions are determined by
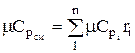 ;
; 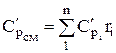 ;
;
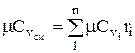 ;
; 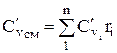
Example 1.5 Dry air by mass consists of g O2 \u003d 23.3% oxygen and g N 2 \u003d 76.6% nitrogen. Determine the composition of air by volume (r O2 and r N 2) and the gas constant of the mixture.
Solution.
1. From Table 1 we find kg/kmol and kg/kmol
2. Determine the volume fractions of oxygen and nitrogen:
1. The gas constant of air (mixture) is determined by the formula:
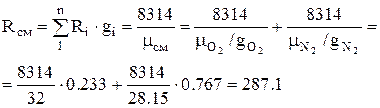 , J/kg K
, J/kg K
Example 1.6. Determine the amount of heat required to heat a gas mixture with a mass of M = 2 kg at P = const, consisting in% by weight: , , , , when the temperature changes from t 1 =900 ° C to t 2 = 1200 ° C.
Solution:
1. Determine the average mass heat capacity of the components that make up the gas mixture at P=const and t 1 =900 o C (from P2):
1.0258 kJ/kg K; =1.1045 kJ/kg K;
1.1078 kJ/kg K; =2.1097 kJ/kg K;
2. We determine the average mass heat capacity of the components that make up the gas mixture at P=const and t 1 =1200 o C (from P2):
1.0509 kJ/kg K; =1.153 kJ/kg K;
1.1359 kJ/kg K; =2.2106 kJ/kg K;
3. We determine the average mass heat capacity of the mixture for the temperature range: t 2 \u003d 1200 ° C and t 1 \u003d 900 ° C:
4. The amount of heat for heating 2 kg of the mixture at P=const:
First law of thermodynamics establishes a quantitative relationship between the change in the internal energy of the system and the mechanical work performed against the forces of external pressure of the environment as a result of the supply of heat to the working fluid.
For a closed thermodynamic system, the equation of the first law has the form
The heat imparted to the working fluid (or system) is used to increase its internal energy (dU) due to an increase in body temperature, and to perform external work (dL) due to the expansion of the working fluid and an increase in its volume.
The first law can be written as dH=dq+VdP=dq-dL 0 ,
where dL 0 \u003d VdP - the elementary work of pressure change is called useful external (technical) work.
dU is the change in the internal energy of the working fluid (system), which includes the energy of the thermal motion of molecules (translational, rotational and vibrational) and the potential energy of the interaction of molecules.
Since the transition of the system from one state to another occurs as a result of heat supply, therefore, the working fluid heats up and its temperature rises by dT and the volume increases by dV.
An increase in body temperature causes an increase in the kinetic energy of its particles, and an increase in body volume leads to a change in the potential energy of particles. As a result, the internal energy of the body increases by dU, so the internal energy U is a function of the state of the body and can be represented as a function of two independent parameters U=f 1 (P,V); U=f 2 (P,T), U=f 3 (υ,T). The change in internal energy in a thermodynamic process is determined only by the initial (U 1) and final (U 2) states, i.e.
In differential form, the change in internal energy is written
a) as a function of specific volume and temperature
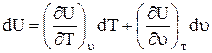
b) as a function of temperature, since , then
For practical calculations, in which it is necessary to take into account the change in C v with temperature, there are empirical formulas and tables of specific internal energy (often molar). For ideal gases, the molar internal energy of the mixture U m is determined by the formula
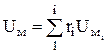 , J/kmol
, J/kmol
For a mixture given by mass fractions . In this way internal energy there is property of the system and characterizes the state of the system.
Enthalpy is the thermal state function introduced by Kamerling-Onnes, (winner Nobel Prize, 1913), which is the sum of the internal energy of the system U and the product of the pressure of the system P and its volume V.
Since the quantities included in it are state functions, therefore H is also a state function, i.e. H \u003d f 1 (P, V); H=f 2 (V,T); H=f 3 (P, T).
The change in enthalpy dH in any thermodynamic process is determined by the initial H 1 and final H 2 states and does not depend on the nature of the process. If the system contains 1 kg of a substance, then the specific enthalpy, J/kg, is applied.
For an ideal gas, the differential equation has the form
accordingly, the specific enthalpy is determined by the formula
The equation of the first law of thermodynamics is dq=dU+Pdυ, when the only type of work is the expansion work Pdυ=d(Pυ)-υdP, then dq=d(U+Pυ)-υdP, whence
In engineering practice, one often has to deal not with homogeneous gases, but with mixtures of chemically unrelated gases. Examples of gas mixtures are: atmospheric air, natural gas, gaseous products of combustion of fuels, etc.
For gas mixtures, the following provisions are valid.
1. Each gas entering the mixture has a temperature, equal to temperature mixtures.
2. Any of the gases included in the mixture is distributed throughout the volume of the mixture and therefore the volume of each gas is equal to the volume of the entire mixture.
3. Each of the gases included in the mixture obeys its own equation of state.
4. The mixture as a whole is like a new gas and obeys its own equation of state.
The study of gas mixtures is based on Dalton's law, according to which, at a constant temperature, the pressure of the mixture is equal to the sum of the partial pressures of the gases included in the mixture:
where p cm is the pressure of the mixture;
p i - partial pressure of the i-th gas included in the mixture;
n is the number of gases included in the mixture.
The partial pressure is the pressure that the gas entering the mixture will exert if it alone occupies the entire volume of the mixture at the same temperature.
Methods for setting gas mixtures
The composition of the gas mixture can be specified by mass, volume and mole fractions.
Mass fractions. The mass fraction of any gas included in the mixture is the ratio of the mass of this gas to the mass of the mixture.
m 1 \u003d M 1 / M cm; m 2 \u003d M 2 / M cm; ..........; m n \u003d M n / M cm,
where m 1 , m 2 , ..., m n - mass fractions gases;
M 1 , M 2 , ..., M n - masses of individual gases;
M cm is the mass of the mixture.
It is easy to see that 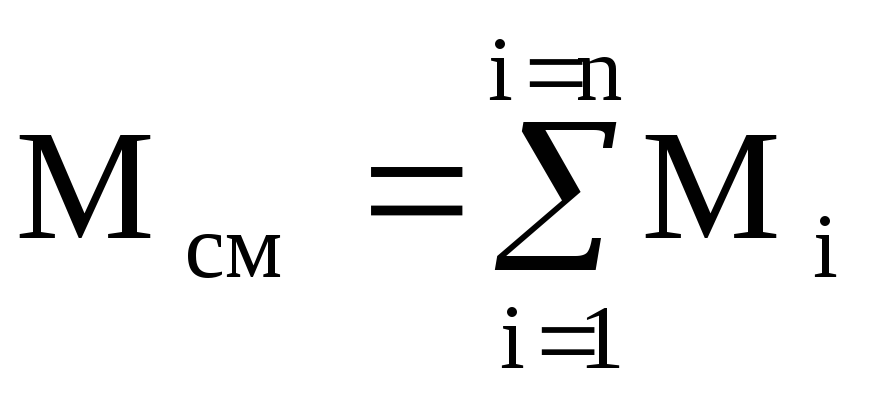 and
and 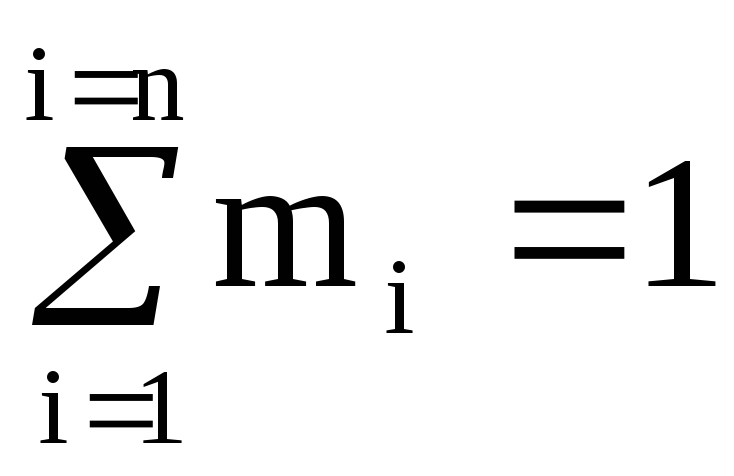 (100%).
(100%).
Volume shares. The volume fraction of any gas included in the mixture is the ratio of the reduced (partial) volume of this gas to the volume of the mixture.
r 1 \u003d V 1 / V cm; r 2 \u003d V 2 / V cm; ........., r n = V n / V cm;
where V 1 , V 2 , ..., V n - reduced volumes of gases;
V cm is the volume of the mixture;
r 1 , r 2 , ..., r n - volume fractions of gases.
The reduced volume is the volume of gas under the conditions of the mixture (at the temperature and pressure of the mixture).
The reduced volume can be represented as follows: if all gases except one are removed from the vessel containing the mixture, and the remaining gas is compressed to the pressure of the mixture while maintaining the temperature, then its volume will be reduced or partial.
It can be proved that the volume of the mixture will be equal to the sum of the reduced volumes of gases.
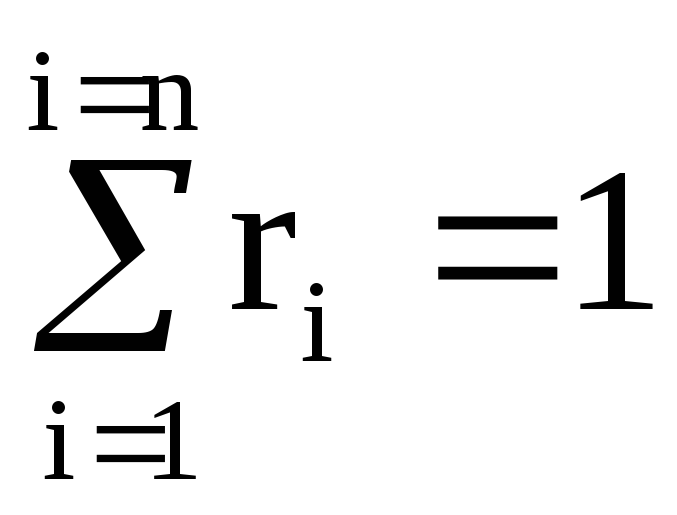 (100%).
(100%).
Mole fractions. The mole fraction of any gas included in a mixture is the ratio of the number of kilomoles of this gas to the number of kilomoles of the mixture.
r 1 \u003d n 1 / n cm; r 2 \u003d n 2 / n cm; ........., r n \u003d n n / n cm,
where r 1 , r 2 , ..., r n - mole fractions of gases;
n cm is the number of kilomoles of the mixture;
n 1 , n 2 , ..., n n is the number of kilomoles of gases.
Specifying a mixture by mole fractions is identical to specifying a mixture by volume fractions, i.e. molar and volume fractions have the same numerical values for each gas included in the mixture.
Gas constant and apparent (average) molecular weight of the mixture. To calculate the gas mixture constant given by mass fractions, we write the equations of state:
for mixture
p cm × V cm = M cm R cm T; (1.9)
for gases
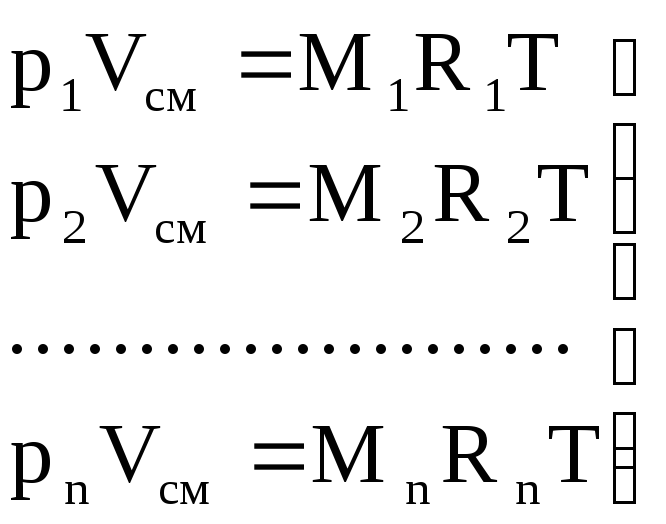 .
(1.10)
.
(1.10)
We sum the left and right parts of equations (1.10)
(p 1 + p 2 + .... + p n) V cm = (M 1 R 1 + M 2 R 2 + ..... + M n R n) T.
Because 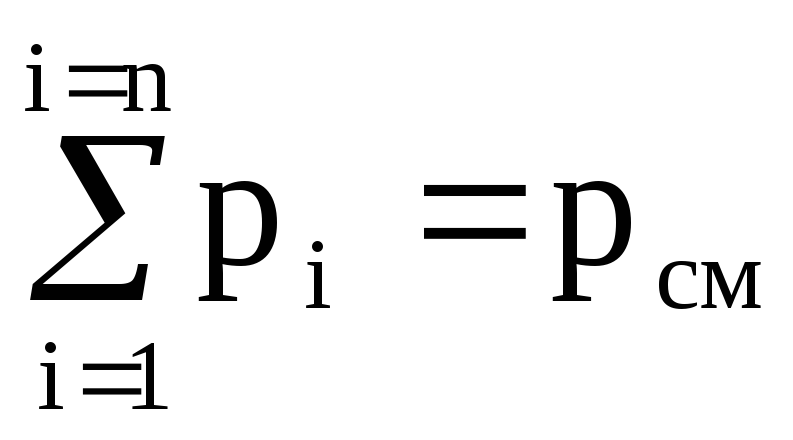 ,
,
then p cm V cm = (M 1 R 1 + M 2 R 2 + ..... + M n R n) T. (1.11)
Equations (1.9) and (1.11) imply that
M cm R cm T \u003d (M 1 R 1 + M 2 R 2 + ..... + M n R n) T.
R cm \u003d M 1 / M cm R 1 + M 2 / M cm R 2 + ...... + M n / M cm R n \u003d
M 1 R 1 + m 2 R 2 + ...... + m n R n
or 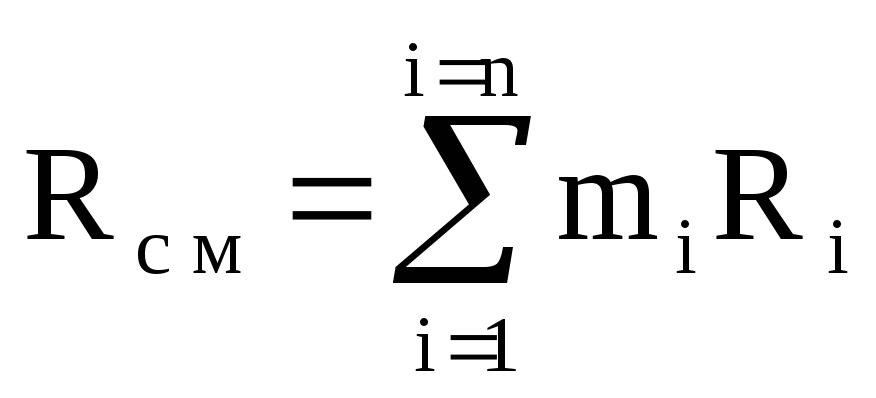 ,
(1.12)
,
(1.12)
where R cm is the gas constant of the mixture.
Since the gas constant of the i-th gas
R i = 8314 / m i ,
then equation (1.12) is rewritten as follows:
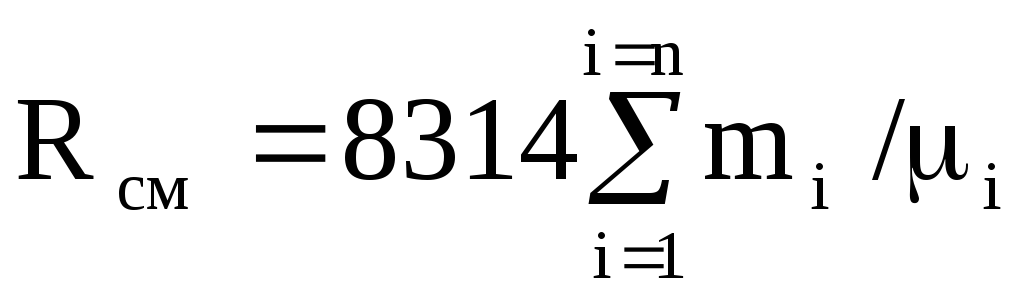 .
(1.13)
.
(1.13)
When determining the parameters of a gas mixture, it is convenient to use a certain conditional value called the apparent (average) molecular weight of the gas mixture. The concept of the apparent molecular weight of a mixture allows us to conventionally consider the mixture as a homogeneous gas, which greatly simplifies the calculations.
For a separate gas, the expression
By analogy, for a mixture, we can write
m cm R cm = 8314, (1.14)
where m cm is the apparent molecular weight of the mixture.
From equation (1.14), using expressions (1.12) and (1.13), we obtain
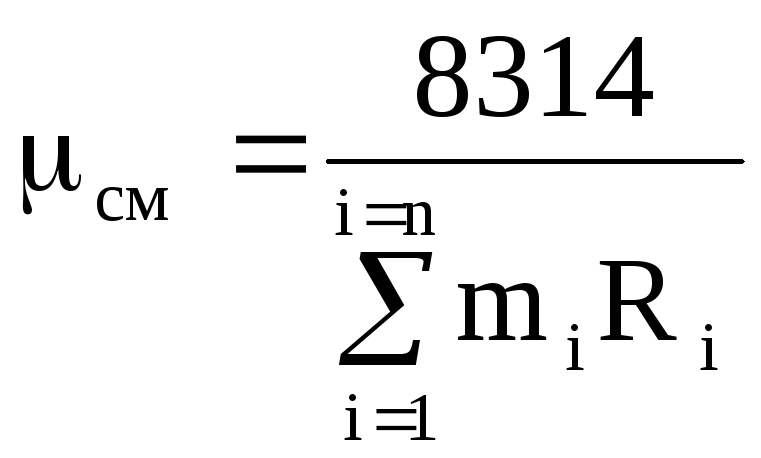 ,
(1.15)
,
(1.15)
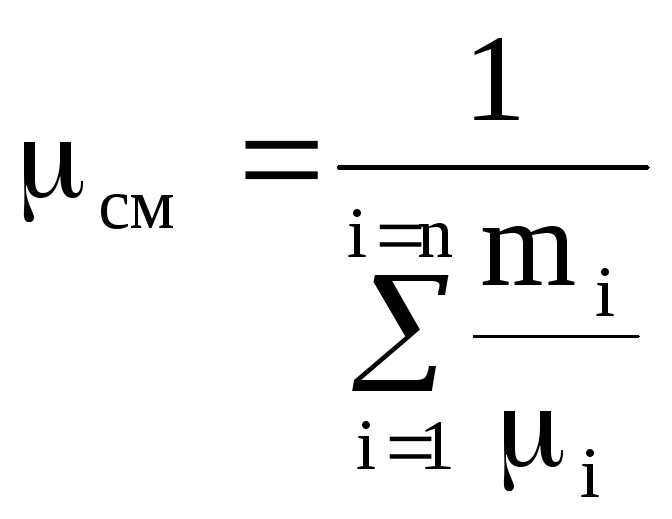 .
(1.16)
.
(1.16)
Arguing in this way, one can obtain formulas for calculating R cm and m cm through volume fractions, formulas for converting mass fractions into volume fractions and, conversely, volume fractions into mass fractions, formulas for calculating the specific volume of a mixture u cm and mixture density r cm through mass and volume fractions and, finally, formulas for calculating the partial pressures of gases included in the mixture, through volume and mass fractions. We present these formulas without derivation in the table.
Formulas for calculating gas mixtures
|
Setting the composition of the mixture |
Transfer from one composition to another |
Density and specific volume of the mixture |
Apparent molecular weight of the mixture |
Gas mixture constant |
Partial pressure |
|
Mass fractions |
|
|
|
|
|
|
Volume fractions |
|
|
|
|
|
Heat capacity of gases
The heat capacity of a body is the amount of heat required to heat or cool the body by 1 K. The heat capacity of a unit amount of a substance is called the specific heat capacity.
So, the specific heat capacity of a substance is the amount of heat that must be reported or subtracted from a unit of a substance in order to change its temperature by 1 K in this process.
Since only specific heat capacities will be considered in what follows, we will refer to the specific heat capacity simply as the heat capacity.
The amount of gas can be given by mass, volume and number of kilomoles. It should be noted that when setting a gas volume, this volume is brought to normal conditions and measured in normal cubic meters (nm 3).
Depending on the method of setting the amount of gas, the following heat capacities are distinguished:
c - mass heat capacity, J / (kg × K);
c¢ - volumetric heat capacity, J / (nm 3 × K);
c m - molar heat capacity, J / (kmol × K).
Between these heat capacities there are the following relationships:
c = c m / m; with m = with × m;
с¢ = с m / 22.4; with m = s¢ × 22.4,
from here 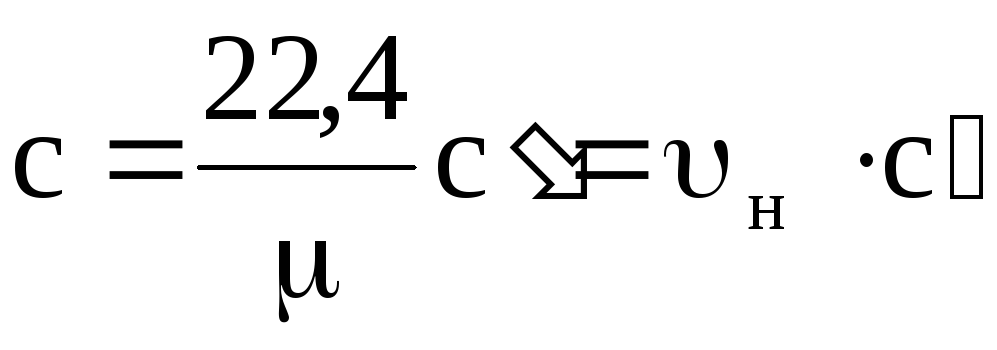 ; s¢ = s × r n,
; s¢ = s × r n,
where u n and r n - specific volume and density under normal conditions.
Isochoric and isobaric heat capacities
The amount of heat imparted to the working fluid depends on the features of the thermodynamic process. Two types of heat capacity are of practical importance depending on the thermodynamic process: isochoric and isobaric.
The heat capacity at u = const is isochoric.
c u - mass isochoric heat capacity,
c¢ u is the volumetric isochoric heat capacity,
c m u is the molar isochoric heat capacity.
The heat capacity at p = const is isobaric.
c p - mass isobaric heat capacity,
c¢ р - volumetric isobaric heat capacity,
c m p - molar isobaric heat capacity.
With the same change in temperature in the process carried out at p = const, more heat is consumed than in the process at u = const. This is explained by the fact that at u = const the heat imparted to the body is spent only on changing its internal energy, while at p = const the heat is spent both on increasing the internal energy and on performing the work of expansion. The difference between the mass isobaric and mass isochoric heat capacities according to the Mayer equation
c p - c u=R. (1.17)
If the left and right sides of equation (1.17) are multiplied by the kilomole mass m, then we get
c m p - c m u= 8314 J/(kmol×K) (1.18)
In thermodynamics and its applications, the ratio of isobaric and isochoric heat capacities is of great importance:
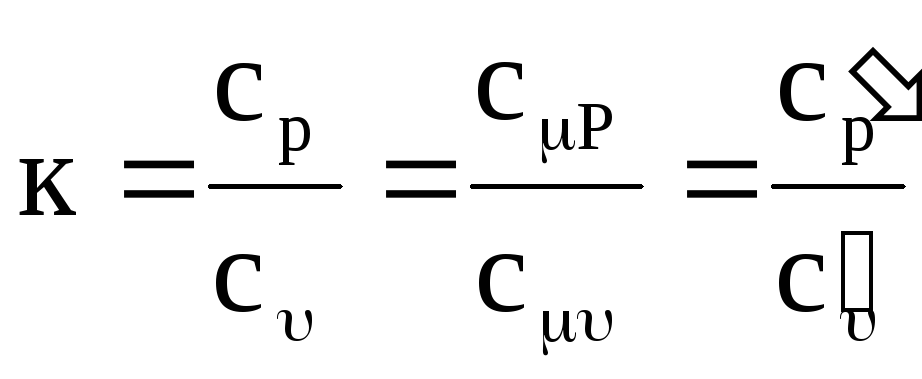 ,
(1.19)
,
(1.19)
where k is the adiabatic exponent.
Calculations show that for monatomic gases k » 1.67, diatomic gases k » 1.4, and triatomic gases k » 1.29.
It is easy to see that the value to temperature dependent. Indeed, it follows from equations (1.17) and (1.19) that
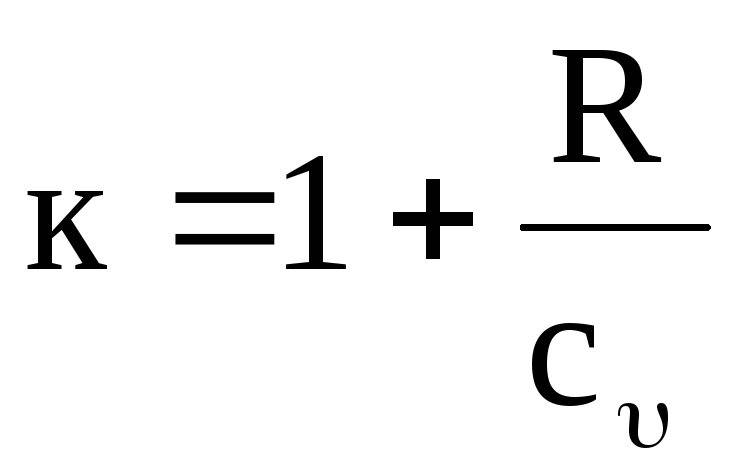 ,
(1.20)
,
(1.20)
and from equations (1.18) and (1.19)
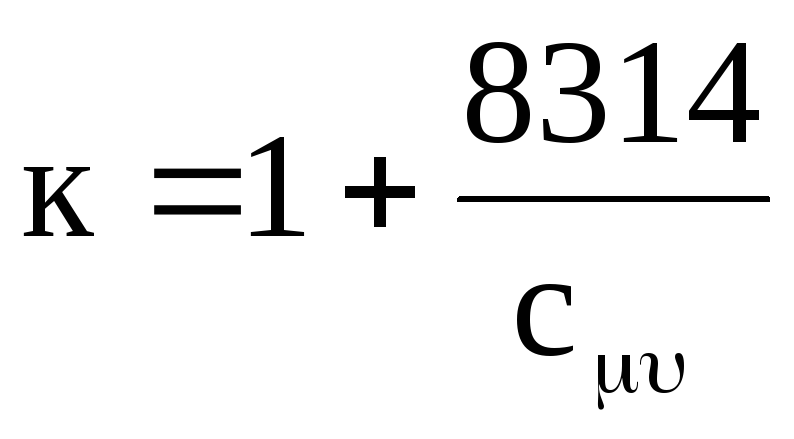 .
(1.21)
.
(1.21)
Since the heat capacities increase with increasing gas temperature, the value of k decreases, approaching unity, but always remains greater than it.
Knowing the value of k, one can determine the value of the corresponding heat capacity. So, for example, from equation (1.20) we have
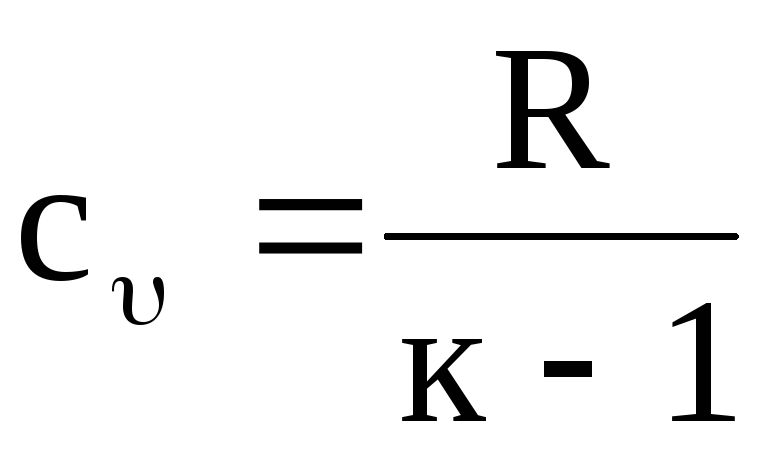 ,
(1.22)
,
(1.22)
and since with p = k × s u, then we get
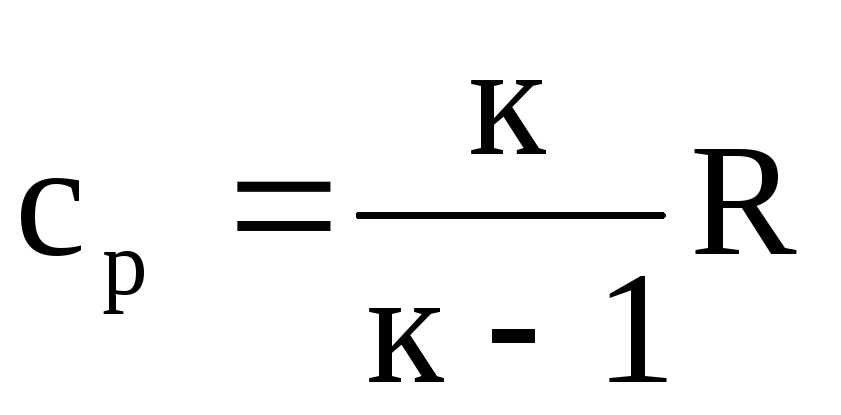 .
(1.23)
.
(1.23)
Similarly, for molar heat capacities, from equation (1.21) we obtain
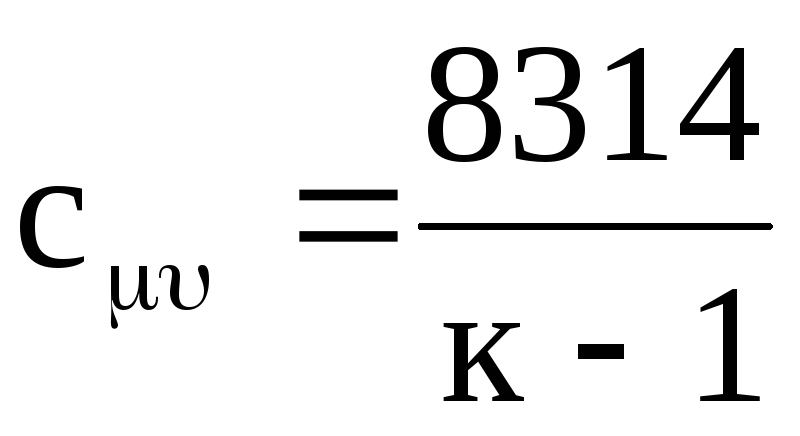 .
(1.24)
.
(1.24)
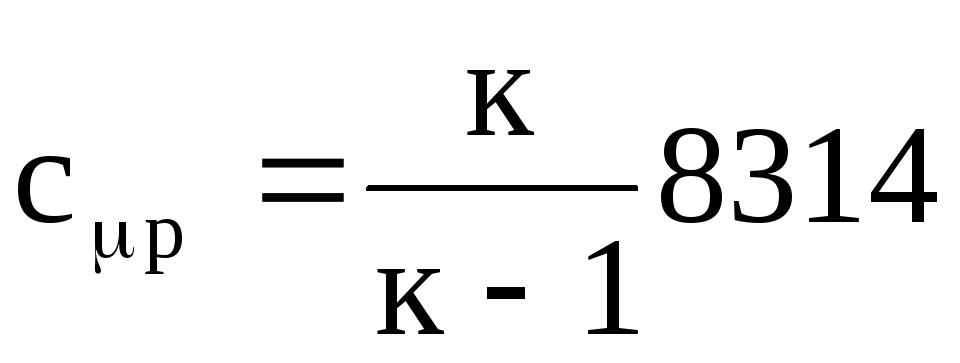 .
(1.25)
.
(1.25)
Average and true heat capacity
The heat capacity of gases depends on temperature and, to some extent, on pressure. The dependence of heat capacity on pressure is small and is neglected in most calculations. The dependence of heat capacity on temperature is significant and must be taken into account. This dependence is quite accurately expressed by the equation
c = a + in t + et 2 , (1.26)
where a, in and e are values that are constant for a given gas.
Often in thermal engineering calculations, the nonlinear dependence (1.26) is replaced by a linear one:
c = a + in t. (1.27)
|
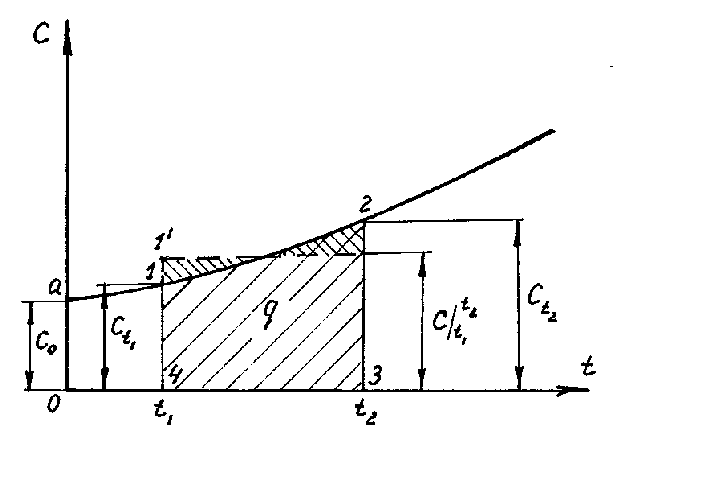
If we construct graphically the dependence of heat capacity on temperature according to equation (1.26), then this will be a curvilinear dependence (Fig. 1.4). As shown in the figure, each temperature value has its own heat capacity value, which is commonly called the true heat capacity. Mathematically, the expression for the true heat capacity is written as follows:
|
|
|
|
Therefore, the true heat capacity is the ratio of an infinitesimal amount of heat dq to an infinitesimal change in temperature dt. In other words, the true heat capacity is the heat capacity of the gas at a given temperature. On fig. 1.4, the true heat capacity at a temperature t 1 is indicated with t1 and is depicted as a segment 1-4, at a temperature t 2 - with t2 and is depicted as a segment 2-3. From equation (1.28) we get dq=cdt. (1.29) In practical calculations, we always determine the amount of heat at the final change |
temperature. It is obvious that the amount of heat q, which is reported to a unit amount of a substance when it is heated from t 1 to t 2, can be found by integrating (1.29) from t 1 to t 2.
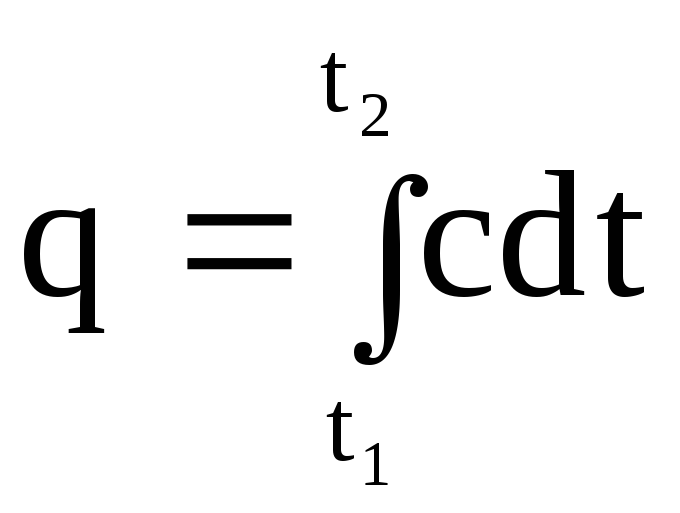 .
(1.30)
.
(1.30)
Graphically, the integral (1.30) is expressed by the area 4-1-2-3. If in expression (1.30) we substitute the value of the true heat capacity according to the linear dependence (1.27), then we obtain
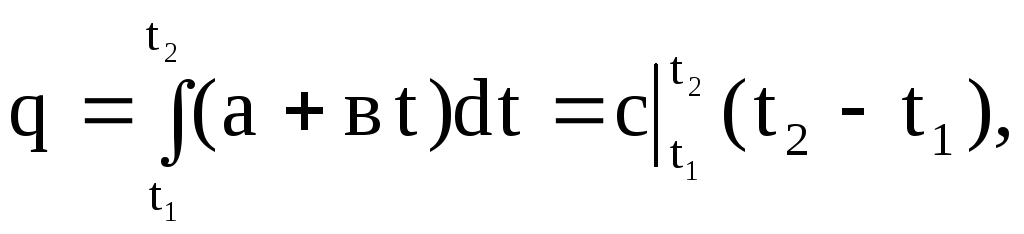 (1.31)
(1.31)
where 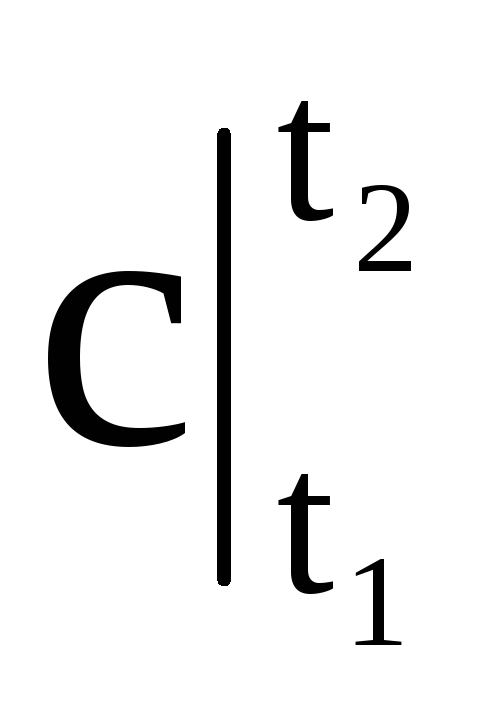 - average heat capacity in the temperature range from t 1 to t 2.
- average heat capacity in the temperature range from t 1 to t 2.
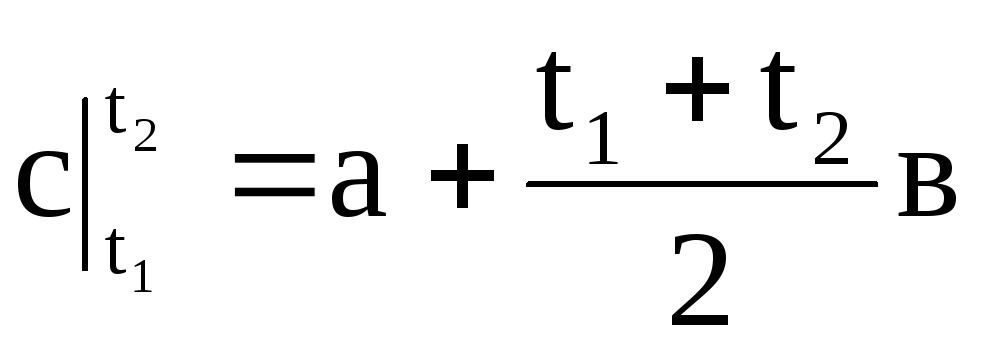 ,
(1.32)
,
(1.32)
Therefore, the average heat capacity is the ratio of the final amount of heat q to the final temperature change t 2 - t 1:
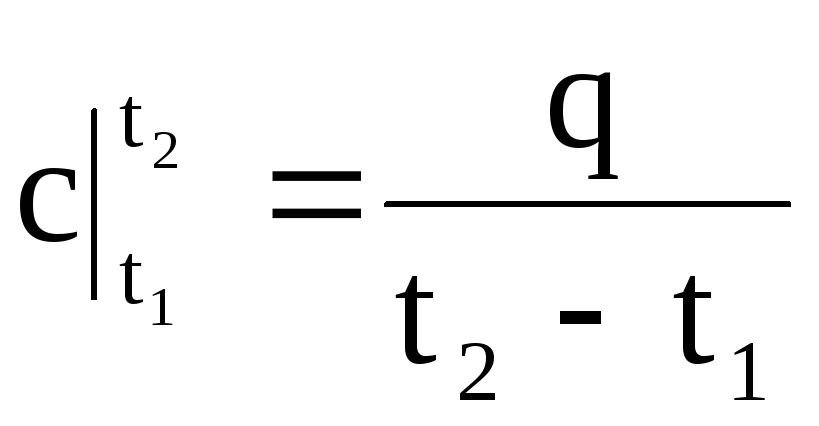 .
(1.33)
.
(1.33)
If, on the basis of 4-3 (Fig. 1.4), a rectangle 4-1¢-2¢-3 is constructed, equal in size to the figure 4-1-2-3, then the height of this rectangle will be equal to the average heat capacity, where 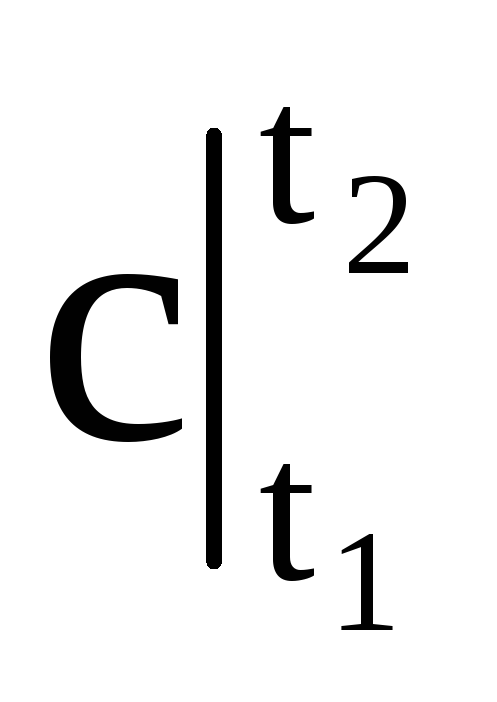 is in the temperature range t 1 - t 2 .
is in the temperature range t 1 - t 2 .
Usually, the values of the average heat capacities are given in tables of thermodynamic properties of substances. However, to reduce the volume of these tables, they provide the values of the average heat capacities determined in the temperature range from 0 ° C to t ° C.
If it is necessary to calculate the value of the average heat capacity in a given temperature range t 1 - t 2, then this can be done as follows.
The area 0a14 under the curve c \u003d f (t) (Fig. 1.4) corresponds to the amount of heat q 1 required to increase the gas temperature from 0 ° C to t 1 ° C.
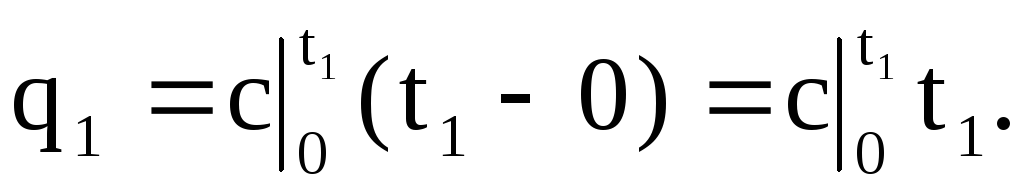
Similarly, the area 0a23 corresponds to q 2 when the temperature rises from 0 o C to t 2 o C:
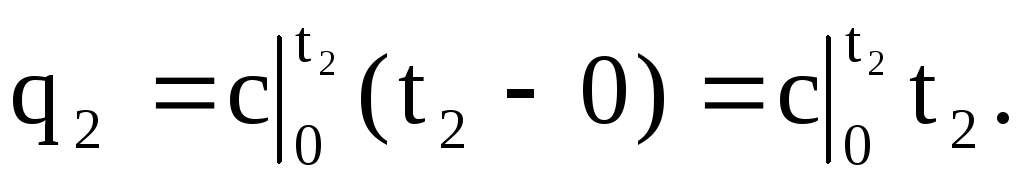
Thus, q \u003d q 2 - q 1 (area 4123) can be represented as
![]() (1.34)
(1.34)
Substituting the value of q according to (1.34) into expression (1.33), we obtain the formula for the average heat capacity in any temperature range:
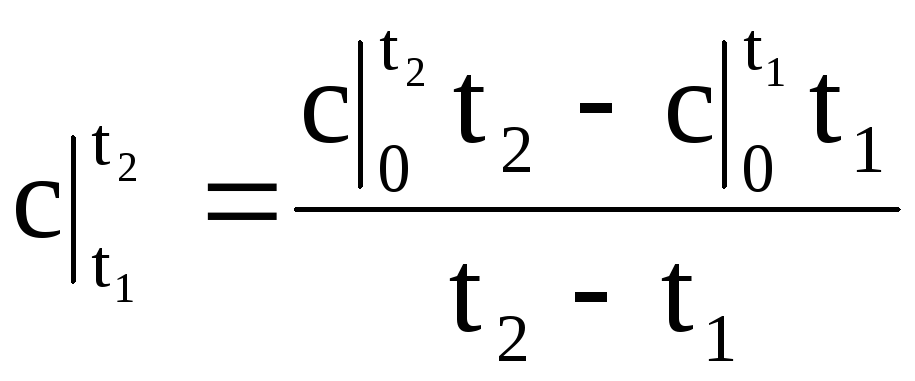 .
(1.35)
.
(1.35)
Thus, the average heat capacity can be calculated from the tabular average heat capacities using equation (1.35). Moreover, we obtain a nonlinear dependence c = f(t). You can also find the average heat capacity using equation (1.32) using a linear relationship. Values a and in in equation (1.32) for various gases are given in the literature.
The amount of heat supplied or removed from the working fluid can be calculated using any of the equations:
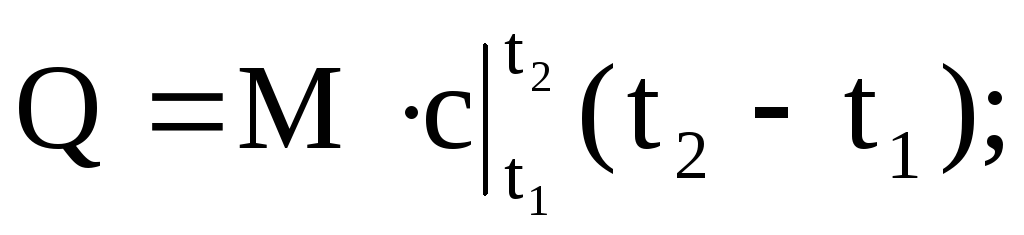 (1.36)
(1.36)
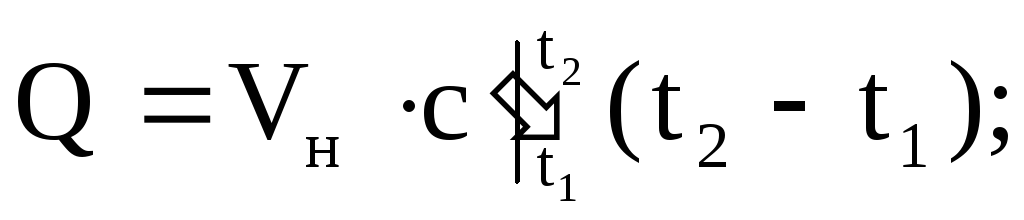 (1.37)
(1.37)
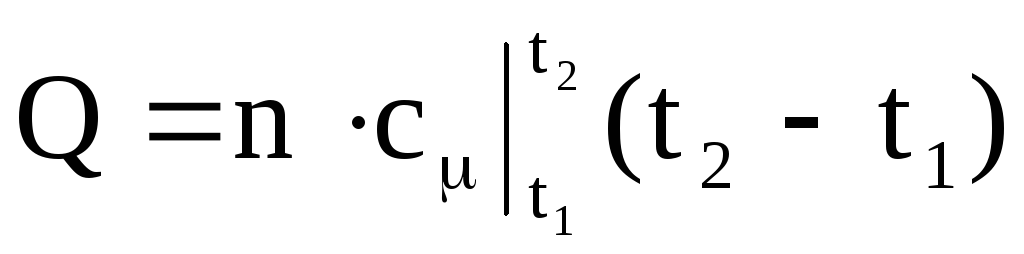 ,
(1.38)
,
(1.38)
where 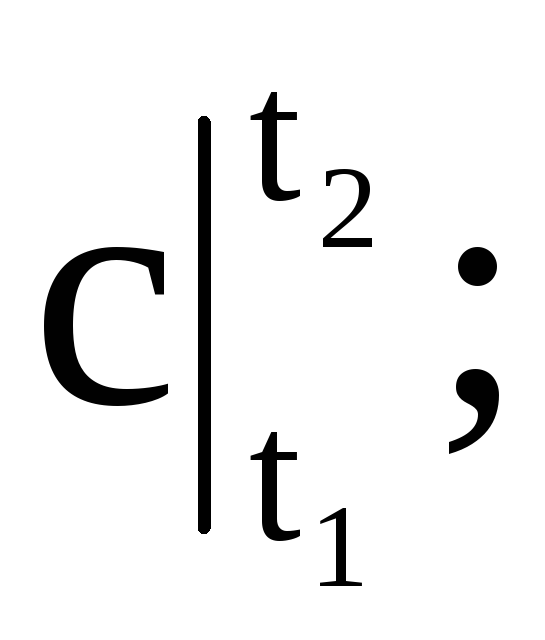
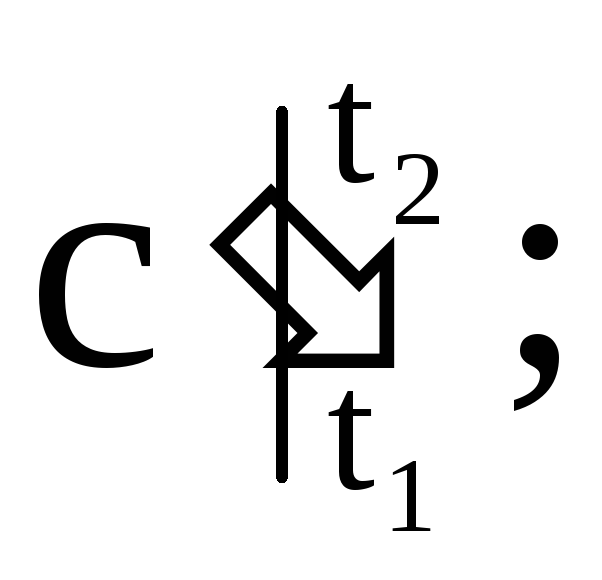
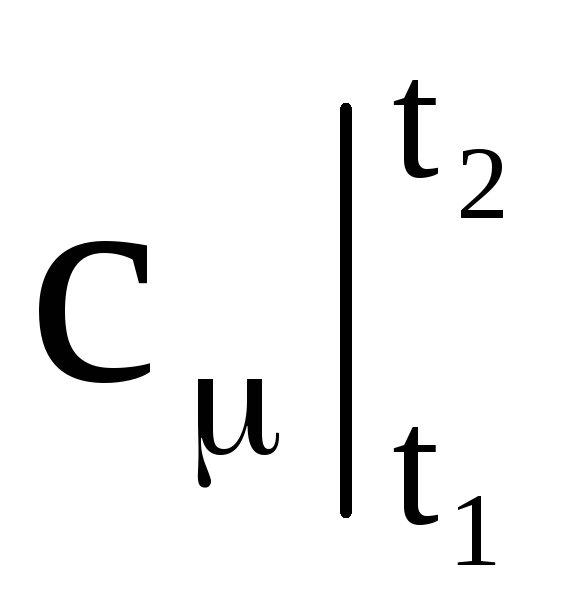 - respectively, the average mass, volume and molar heat capacity; M is the mass of gas; n is the number of kilomoles of gas; V n - the volume of gas under normal conditions.
- respectively, the average mass, volume and molar heat capacity; M is the mass of gas; n is the number of kilomoles of gas; V n - the volume of gas under normal conditions.
The volume of gas V n can be found as follows. Having written the equation of state for the given conditions: pV = MRT and for normal conditions: p n V n = MRT n, we attribute the second equation to the first:
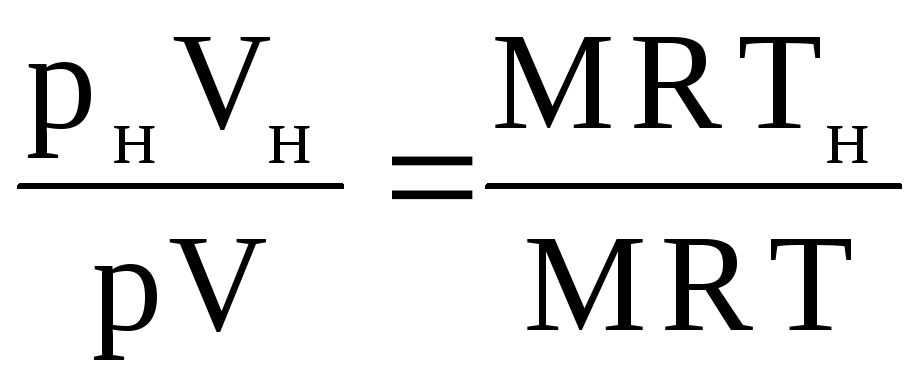 ,
,
from here 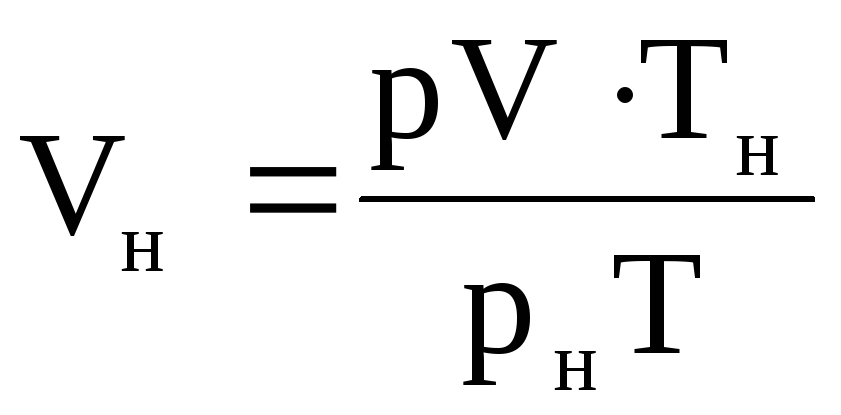 .
(1.39)
.
(1.39)
Heat capacity of gas mixtures
The heat capacity of a gas mixture can be calculated if the composition of the mixture is given and the heat capacities of the components included in the mixture are known.
To heat a mixture of mass M cm by 1 K, the temperature of each of the components must also be increased by 1 K. At the same time, the amount of heat equal to c i M i is spent on heating the i-th component of the mixture with mass М i . For the entire mixture, the amount of heat 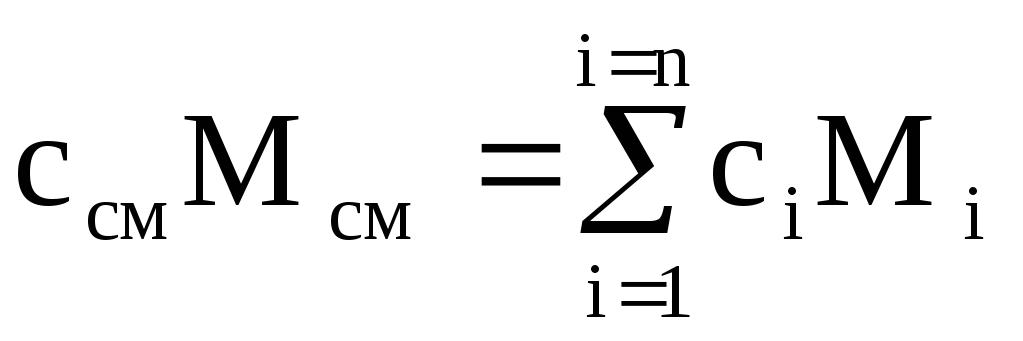 ,
,
where c i and c cm are the mass heat capacities of the i-th component and mixture.
Dividing the last expression by M cm, we obtain the calculation formula for the mass heat capacity of the mixture:
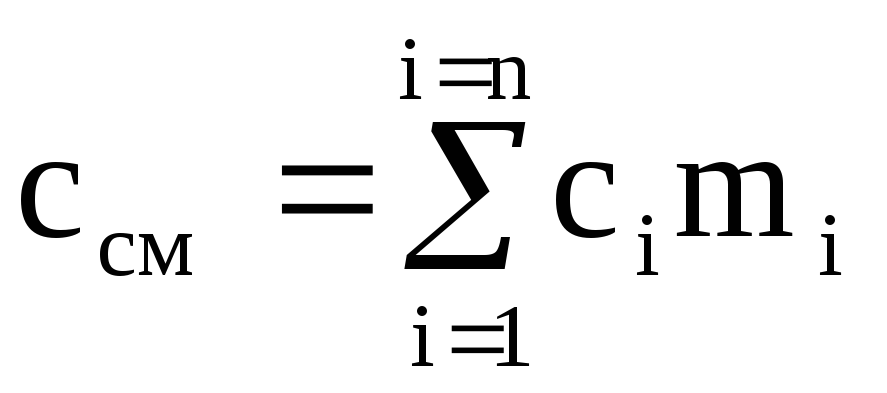 ,
(1.40)
,
(1.40)
where m i is the mass fraction of the i-th component.
Arguing similarly, we find the volumetric heat capacity c¢ cm and the molar heat capacity c m cm of the mixture:
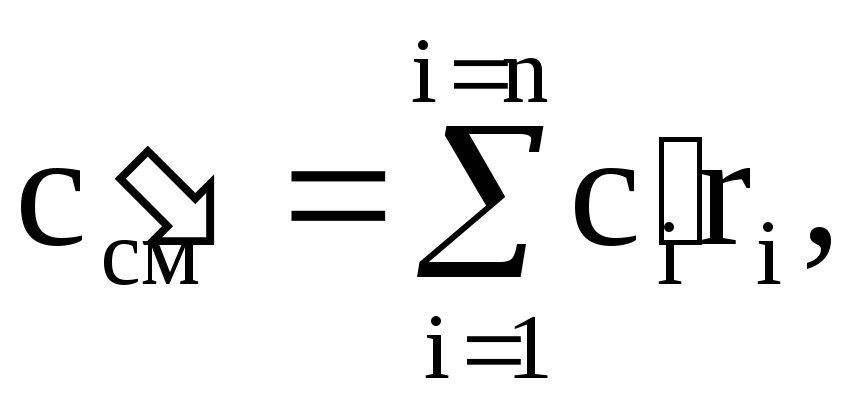 (1.41)
(1.41)
where c¢ i - volumetric heat capacity of the i-th component, r i - volume fraction of the i-th component,
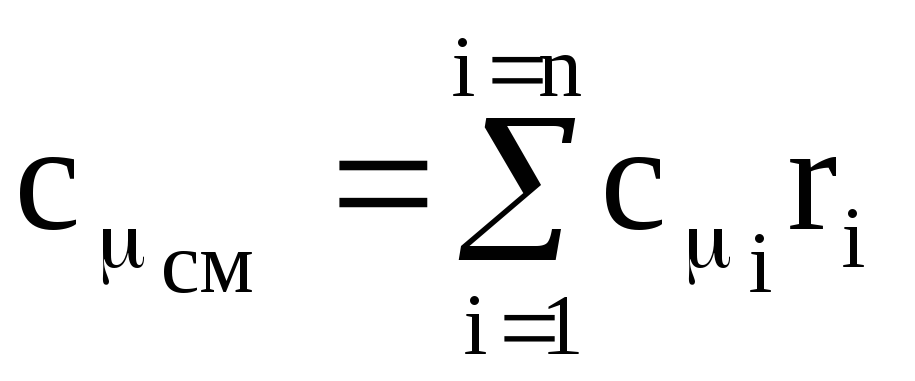 ,
(1.42)
,
(1.42)
where c m i is the molar heat capacity of the i-th component,
r i - mole (volume) fraction of the i-th component.
Practical work№ 2
Topic: Heat capacity, enthalpy, mixtures of ideal gases, internal energy, work, thermodynamic processes.
The purpose of the work: Consolidation of knowledge gained during theoretical training, acquisition of skills in the implementation of heat engineering calculations.
I. Basic definitions, formulas and equations
1. Mixtures of ideal gases
A gas mixture is a mechanical mixture of several gases that do not chemically interact with each other. Each of the gases in the mixture is called a gas component; behaves as if there were no other gases in the mixture, i.e. evenly distributed throughout the mixture. The pressure exerted by each gas of the mixture on the walls of the vessel is called partial pressure. The basic law for mixtures of ideal gases is Dalton's law, according to which the pressure of the mixture is equal to the sum of the partial pressures of the gases that form the mixture:
2. Internal energy
The internal energy of the body is a combination of the kinetic energy of the movement of the microparticles that make up the body, and their potential energy. interaction defined. forces of mutual attraction or repulsion. It is impossible to determine the absolute value of the internal energy, therefore, in thermodynamic calculations, it is not the absolute value of the internal energy that is calculated, but its change, i.e.
![]() or
or ![]()
where U 1 and U 2 - the internal energy of the initial and final state of the working fluid (gas);
u 1 and and 2 - beats. internal energy of the initial and final state of the working fluid.
It follows from this that the change in internal energy does not depend on the nature and path of the process, but is determined by the state of the working fluid at the beginning and end of the process of change.
A feature of an ideal gas is the absence of forces of molecular interactions in it, and hence the absence of internal potential energy, i.e. U n \u003d 0 and U „ \u003d 0. Therefore, the internal energy of an ideal gas:
U=U k =f(T) unu u=uk =f(T).
H. Gas work.
In thermodynamics, any change in the state of the working fluid as a result of the exchange of energy with environment called a process. In this case, the main parameters of the working body are changed:
The transformation of heat into mechanical work is associated with the process of changing the state of the working fluid. The processes of changing the state of a gas can be expansion and contraction processes. For an arbitrary mass of gas M (kg), the work is equal to:
L \u003d M l \u003d Mp (v 2 - v 1) \u003d, J
where l \u003d p (v 2 -v 1) J / kg is the work of 1 kg of gas or specific work.
4. Gas enthalpy,
Enthalpy is a parameter that characterizes the potential energy of the connection of the working fluid (gas) with the environment. Enthalpy and specific enthalpy:
I \u003d U + pV, J and i i \u003d and + pv, J / kg.
5. Heat capacity.
Specific heat capacity is the amount of heat that must be supplied to 1 kg of gas in order to heat it by 1 ° C in a given temperature range.
Specific heat capacity is mass, volumetric and kilomol. There is a connection between mass C, volume C and kilomol C heat capacities:
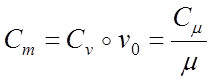 ;
; 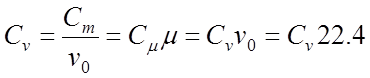
where Vo 22.4 m 3 / kmol - beats. volume of gas under normal conditions.
Mass ud. heat capacity of the gas mixture:
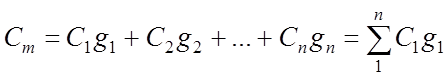
Volumetric specific heat of the gas mixture:
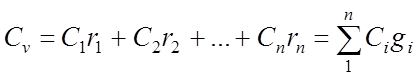
Kilomolar specific heat of the gas mixture:
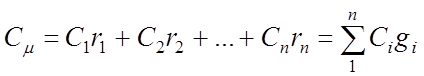
6. Equation for determining the amount of heat
The amount of heat given off or taken in by the working fluid (gas) can be determined by the equation:
Q \u003d M C m (t 2 -t 1), J or Q \u003d VC (t-t), J, where M and V are the weight or volume amount of gas, kg or m 3;
t u t - gas temperature at the end and at the beginning of the process ° С;
C and C - mass and volume average beats. heat capacity of gas
At t cp \u003d J / kgK or J / m 3 K
7. First law of thermodynamics
This law considers the interconversions of heat and mechanical work. According to this law, heat is converted into mechanical work and vice versa, mechanical work into heat in strictly equivalent quantities. The equivalence equation for heat and work has the form:
Taking into account the principle of equivalence of heat and work, the heat balance equation for an arbitrary mass of gas:
Q \u003d U + L and q \u003d u + l \u003d u -u + l
Problem solvingII
Task #1 (#1)
Atmospheric dry air has the following approximate mass composition: g 02 =23.2%, g N 2 =76.8%.
Determine the volumetric composition of air, its gas constant, apparent molecular weight, partial pressure of oxygen and nitrogen, if air is P = 101325 Pa using a barometer.
I determine the volumetric composition of air:
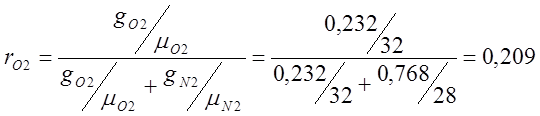 ;
;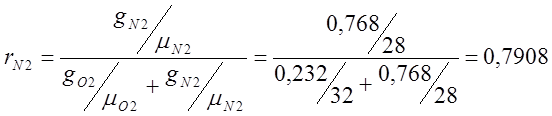 ;
;
where r is the mass fraction;
m is the relative molecular weight;
g is the volume fraction.
m air. =m O2 r O2 +m N2 r N2 = 32 0.209 + 28 0.7908=6.688+22.14=28.83;
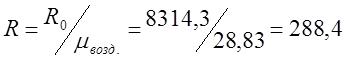
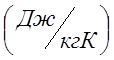 ;
;
where R 0 is the gas constant.
I determine the partial pressures of various gases:
P O 2 \u003d P cm r O2 \u003d 101325 0.209 \u003d 21176.9 (Pa);
P N 2 \u003d P cm r N 2 \u003d 101325 0.7908 \u003d 80127.81 (Pa);
where P O 2 , P N 2 - partial pressure;
P cm is the pressure of the mixture.
Task #2 (#2)
The vessel is divided by a partition into 2 parts, the volumes of which are V 1 =1.5 m 3 and V 2 =1.0 m 3 . The first part of the volume V 1 contains CO 2 at P 1 =0.5 MPa and t 1 =30°C; the second part of the volume V 2 contains O 2 at P 2 =0.2 MPa and t 2 =57°C. Determine the mass and volume fractions of CO 2 and O 2, the apparent molecular weight of the mixture and its gas constant after the partition is removed and the mixing process is completed.
I determine individual gas constants:
To do this, I determine the relative molecular weight: m (CO 2) \u003d 32 + 12 \u003d 44; m(O 2)=32;
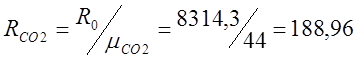
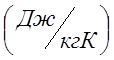 ;
;
![]()
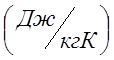 ;
;
According to the characteristic equation of Klaiperon, I determine the masses of gases:
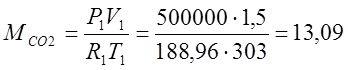 (kg);
(kg);
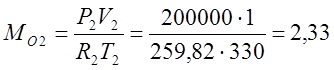 (kg);
(kg);
I determine the mass fractions:
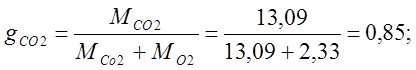
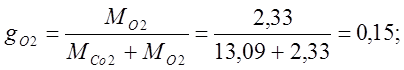
I determine the volume fractions:
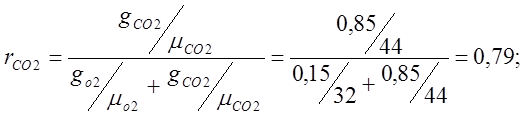
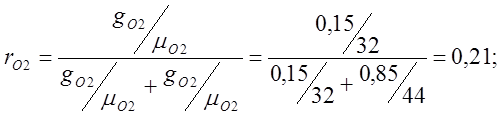
Determine the apparent molecular weight of air:
m air. \u003d m O2 r O 2 + m CO2 r CO2 \u003d 32 0.21 + 44 0.79 \u003d 6.72 + 34.74 \u003d 41.48;
I determine the individual gas constant for air (R):
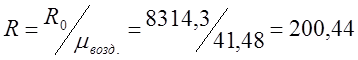
 ;
;
Task #3 (#6)
In a vessel with a volume of 300 l there is oxygen at a pressure P 1 \u003d 0.2 MPa and t 1 \u003d 20 0 C. How much heat must be supplied so that the temperature of oxygen rises to t 2 \u003d 300 0 C? What pressure will be established in the vessel? For calculation, take the average volumetric specific heat of oxygen at n.o. C 02 \u003d 0.935 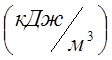
According to Charles's law, I determine the final pressure of the process:
; 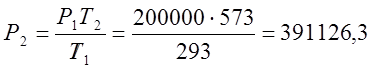 (Pa);
(Pa);
where P, T are gas parameters.
I determine the individual gas constant for oxygen (R):
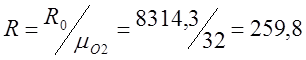
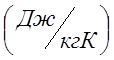 ;
;
Since the process is isochoric, I determine the amount of heat that needs to be supplied according to the appropriate formula: Q v \u003d M C cv (T 2 -T 1) for this, according to the Claiperon characteristic equation, I determine the mass of gas
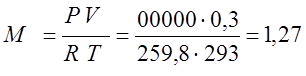 (kg); Q v \u003d M C cv (T 2 -T 1) \u003d 1.27 935 280 \u003d 332486 (J).
(kg); Q v \u003d M C cv (T 2 -T 1) \u003d 1.27 935 280 \u003d 332486 (J).
Task #4 (#7)
How much heat must be expended to heat 2m 3 of air at a constant overpressure P ex. \u003d 0.2 MPa from a temperature of 100 0 C to a temperature of 500 0 C. What work will the air do in this case? For calculation, take: atmospheric pressure P at. \u003d 0.1 MPa, average mass isobaric heat capacity of air C pm \u003d 1.022 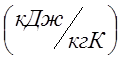 ; calculate the gas constant bearing in mind that the apparent molecular weight of air M air. =29.
; calculate the gas constant bearing in mind that the apparent molecular weight of air M air. =29.
I determine the individual gas constant for air:
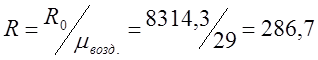
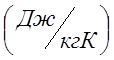 ;
;
The absolute pressure is equal to the sum of the excess and atmospheric P=P est. + P at. =0.1+0.2=0.3 MPa
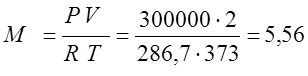 (kg);
(kg);
Since the process is isobaric, I determine Q and L according to the corresponding formulas:
according to the Gay-Lussac law, I determine the final volume:
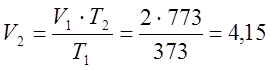 m 3;
m 3;
Q \u003d M C pm (T 2 -T 1) \u003d 5.56 1022 400 \u003d 2272928 (J);
L \u003d P (V 2 -V 1) \u003d 300000 2.15 \u003d 645000 (J).
Task #5 (#8)
There is air in the cylinder at a pressure P=0.5 MPa and a temperature t 1 =400 0 C. Heat is removed from the air at P=const so that at the end of the process the temperature t 2 =0 0 C is set. The volume of the cylinder in which air V 1 \u003d 400l.
Determine the amount of heat removed, the final volume, the change in internal energy and the perfect work of compression C pm =1.028  .
.
Since the process is isobaric, then according to the Gay-Lussac law I determine the final volume:
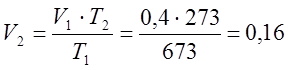 m 3;
m 3;
According to the characteristic equation of Klaiperon, I determine the mass of gas:
From the previous problem R=286.7 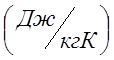
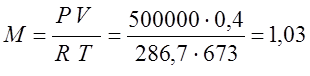 (kg);
(kg);
I determine the amount of heat that is released:
Q=M C pm (T 2 -T 1)=1.03 1028 (273-673)=-423536 (J);
I determine the amount of work spent:
L=P (V 2 -V 1)= 500,000 (0.16-0.4)=-120,000 (J);
From the equation by which the total amount is determined, I determine the change in the amount of internal energy:
![]() ; (J)
; (J)
Problem #6 (#9)
Air having a volume V 1 =0.02 m3 at pressure P 1 =1.1 MPa and t 1 =25 s expands in the cylinder with a movable piston to a pressure P 2 =0.11 MPa. Find the final volume V 2, the final temperature t 2 , the work done by the air, and the heat supplied, if the expansion in the cylinder occurs:
a) isothermally
b) adiabatically with adiabatic exponent k=1.4
c) polytropic with polytropic index n=1.3
Isothermal process:
P 1 / P 2 \u003d V 2 / V 1
V 2 \u003d 0.02 1.1 / 0.11 \u003d 0.2M 3
Q=L=RMT 1 Ln(V 2 /V 1)=P 1 V 1 Ln(V 2 /V 1)=1.1 10 6 0.02Ln(0.2/0.02)=22000J
adiabatic process:
V 1 / V 2 \u003d (P 2 / P 1) 1 / k
V 2 \u003d V 1 / (P 2 / P 1) 1 / k \u003d 0.02 / (0.11 / 1.1) 1 / 1.4 \u003d 0.1036M 3
T 2 /T 1 \u003d (P 2 /P 1) k-1 / k
T 2 \u003d (P 2 / P 1) k-1 / k T 1 \u003d (0.11 / 1.1) 1.4-1 / 1.4 298 \u003d 20.32k
C v \u003d 727.4 J / kg k
L \u003d 1 / k-1 (P 1 V 1 -P 2 V 2) \u003d (1 / 1.4-1) (1.1 10 6 0.02 -0.11 10 6 0, 1)=2.0275 10 6 J
Polytropic process:
V 1 / V 2 \u003d (P 2 / P 1) 1 / n
V 2 \u003d V 1 / (P 2 / P 1) 1 / n \u003d 0.02 / (0.11 / 1.1) 1 / 1.3 \u003d 0.118M 3
T 2 /T 1 \u003d (P 2 /P 1) n-1 / n
T 2 \u003d (P 2 / P 1) n-1 / n T 1 \u003d (0.11 / 1.1) 1.3-1 / 1.3 298 \u003d 175k
L \u003d 1 / n-1 (P 1 V 1 -P 2 V 2) \u003d (1 / (1.3-1)) (1.1 10 6 0.02 -0.11 10 6 0.118)=30000J
Q=(k-n/k-1) l M=((1.4-1.3)/(1.4-1)) 30000=7500J
Literature:
1. Energy, Moscow, 1975.
2. Litvin A.M. "Theoretical foundations of heat engineering", publishing house "Energy", Moscow, 1969.
3. Tugunov P.I., Samsonov A.A., "Fundamentals of heat engineering, heat engines and steam power facilities", Nedra publishing house, Moscow, 1970.
4. Krutov V.I., "Heat engineering", publishing house "Engineering", Moscow, 1986.
Practical work No. 1
Topic: Ideal gases and gas mixtures. Heat capacity of gases
Target: give students the concept of an ideal gas and gas mixtures, as well as the heat capacity of gases.
Brief theoretical information
When calculating ideal gases and gas mixtures, as well as the heat capacity of gases, it is necessary to know and use the following formulas:
Equations of state for ideal gases:
– for 1 kg of gas
, (1.1)
- for m kg of gas
, (1.2)
– for 1 mole of gas
, (1.3)
where is the molar volume, m 3 /mol; is the universal (molar) gas constant, J/(mol K).
Universal gas constant = 8.314 J/(mol. TO).
Specific gas constant, J/(kg K),
, (1.4)
where is the molar mass, kg/mol
, (1.4a)
where is the relative molecular weight of the substance.
Thermodynamic temperature, K,
, (1.5)
where is the temperature in degrees Celsius, 0 C.
It is customary to bring the volume of gas to the so-called normal conditions, under which the gas pressure \u003d 101.3 kPa, and the temperature \u003d 0 0 C.
Gas mixture pressure
, (1.6)
where is the partial pressure of the component.
For gas mixture
, (1.7)
where is the mass of the component;
, (1.7a)
where is the partial (reduced) volume of the component, m 3 .
Gas mixture density
, (1.8)
where is the volume fraction of the component; is the density of this component, kg/m 3 ;
, (1.8a)
where is the mass fraction of the component.
Apparent molar mass of a mixture of ideal gases
, (1.9)
where is the molar mass of the component;
. (1.9a)
The ratio between mass and volume fractions
. (1.10)
Partial pressure of the component
. (1.11)
The heat capacity determines the amount of heat that must be supplied to the body (to the system) in order to increase the temperature by 1 0 C (per 1 K).
There is a functional relationship between these heat capacities
. (1.12)
Of particular importance in thermal calculations are the heat capacities of gas in processes at constant pressure and constant volume - isobaric and isochoric heat capacities, respectively. They are connected by the Mayer equation:
– for 1 kg of gas
, (1.13)
where and are the isobaric and isochoric specific heat capacities;
– for 1 mole of gas
, (1.13a)
where and are the isobaric and isochoric molar heat capacities.
The ratio of these heat capacities is called the adiabatic exponent
. (1.14)
The average heat capacity in the temperature range from to is usually calculated as
, (1.15)
where and are the average heat capacities in the temperature range from 0 to 0 С and from 0 to 0 С.
Heat capacities of a mixture of gases:
– specific
, (1.16)
where – specific heat capacity component;
– volumetric
, (1.16a)
where is the volumetric heat capacity of the component;
– molar
, (1.16b)
where is the molar heat capacity of the component.
Guidelines to problem solving
Task number 1.
The compressor pumps air in the amount of 4 m 3 /min at 17 0 C and a pressure of 100 kPa into a tank with a volume of 10 m 3 . How long will it take for the pressure in the tank to increase from 0.1 to 0.9 MPa? When calculating, assume that the air temperature in the tank does not change and is equal to 17 0 C.
Solution
The mass of air in the tank at the beginning of the compressor operation according to the formula (1.2)
kg,
where accepted:
287 kJ/(kg . K) - specific gas constant of air (Appendix B);
17 + 273.15 = 290.15 K - according to equation (1.5).
The mass of air in the tank when the final pressure is reached = 0.9 MPa according to the formula (1.2)
kg.
Air density at its initial parameters according to dependence (1.1)
kg / m 3.
According to the condition of the problem, the volume flow of the compressor is set = 4 m 3 /min, it is required to determine its mass feed
kg/min.
Compressor running time when air is forced into the tank
min.
Answer: In 20 minutes, the pressure in the tank will increase from 0.1 to 0.9 MPa.
Task number 2.
Determine the specific and volumetric heat capacities of air in processes at constant pressure and volume, assuming that the heat capacity is constant. Air density under normal conditions = 1.29 kg/m 3 .
Solution
We write out for air the relative molecular weight = 28.96 (Appendix B) and the value of molar heat capacities as for a diatomic gas = 29.1 J / (mol. K) and \u003d 20.8 J / (mol. K) (Appendix B).
According to formula (1.4a), we determine:
– molar mass of air
kg/mol
Calculate by formula (1.12):
– isobaric specific heat
J / (kg. K) \u003d 1.005 kJ / (kg. K),
– isobaric volumetric heat capacity
kJ / (m 3. K),
– isochoric specific heat
J / (kg K) \u003d 0.718 kJ / (kg. TO),
– isochoric volumetric heat capacity
kJ / (m 3. K).
Answer: The specific heat capacity is 0.718 kJ/(kg . K), and the volumetric heat capacity is 0.926 kJ / (m 3. K).
Tasks for independent solution
Task number 1.
Find the density of carbon dioxide under normal conditions.
Task number 2.
What is the volume of 100 kg of nitrogen at 70 0 C and a pressure of 0.2 MPa?
Task number 3.
Determine the mass of air in an auditorium with an area of 120 m 2 and a height of 3.5 m. The air temperature in the audience is 18 0 C, and the barometric pressure is 100 kPa.
Task number 4.
Determine the number of atoms in an oxygen molecule if in a volume of 10 liters at a temperature of 30 0 C and a pressure of 0.5 MPa is 63.5 g of oxygen.
Task number 5.
In a tank with a capacity of 8 m 3 there is air at a pressure of 10 MPa and at a temperature of 27 0 C. After some of the air was used up, the pressure dropped to 5 MPa, and the temperature to 20 0 C. Determine the mass of air used.
Task #6
Compressor pumps gas into a 10 m tank 3 . In this case, the pressure in the reservoir increases from 0.2 to 0.7 MPa at a constant gas temperature of 20 0 C. Determine the operating time of the compressor if its supply is 180 m 3 /h The feed is determined under normal conditions.
Task number 7.
The compressor pumps air into a 7 m tank 3 , while the pressure in the tank increases from 0.1 to 0.6 MPa. The temperature also rises from 15 to 50 0 C. Determine the running time of the compressor if its flow is 30 m 3 /h, being related to normal conditions: 0.1 MPa and 0 0 C.
Task number 8.
To determine the heat of combustion of fuel, a 0.4-liter calorimetric bomb filled with oxygen is used. During the charge, an oxygen pressure in the bomb is reached, equal to 2.2 MPa. Oxygen comes from a 6 liter cylinder. How many charges will there be enough oxygen in the cylinder if its initial pressure is 12 MPa? When calculating, take the temperature of oxygen both in the cylinder and when charging the bomb equal to 20 0 C.
Task number 9.
Starting a stationary engine is carried out with compressed air from a 40-liter cylinder. 0.1 m3 of air is consumed for 1 start 3 determined under normal conditions. Determine the number of engine starts if the pressure in the cylinder decreases from 2.5 to 1 MPa. Take the air temperature equal to 10 0 C.
Task number 10.
The gaseous products of fuel combustion are cooled in an isobaric process from temperature to temperature. The composition of gases is given in volume fractions: , and. Find the amount of heat given off by 1 m 3 combustion products. The volume is determined under normal conditions.
Take the initial data according to the table. 1.1 depending on the cipher (option number). The calculation is carried out using the average heat capacities.
Table 1.1. Initial data
test questions
1. Give the definition of an ideal gas and indicate its differences from a real gas.
2. What is the difference between the gas constant and the universal gas constant?
3. What is called the partial pressure of a gas in a mixture, does it exist physically and how is it determined?
4. What is called the partial volume of gas in a mixture, does it exist physically and how is it determined?
5. How to determine the volume fraction of a gas in a mixture if its mass fraction is known?
6. What characteristics of ideal gases determine the numerical values of their specific molar isobaric and isochoric heat capacities.
Send your good work in the knowledge base is simple. Use the form below
Students, graduate students, young scientists who use the knowledge base in their studies and work will be very grateful to you.
Hosted at http://www.allbest.ru/
Ministry of Education and Science of the Russian Federation
Federal State Budgetary Educational Institution
Higher education
Volgograd State Technical University
Kirov Evening Faculty
Semester work on discipline:
Heat engineering
On the topic:
FUEL, GAS MIXTURES AND HEAT CAPACITY
Completed by: student gr.TVB-385
Sheludchenko B.D.
Checked by: Assoc. Goryunov V.A.
Volgograd 2015
Condition
fuel combustion temperature oxidizer
In an industrial furnace, fuel (ethanol) is burned at constant pressure. Air is used as an oxidant at a temperature T 1 =660K. The coefficients of excess air are given: a= 1.0 and the coefficient of completeness of fuel combustion w=0.9. Determine the theoretical value of the maximum combustion temperature Tg. Ignore the heat introduced by the fuel.
Tab. No. 1. Composition and calorific value of fuel
Tab. No. 2. Formulas for average isochoric mass heat capacities (c v)
|
Heat capacity kJ/kg*K |
|||
|
0.691 + 7.1 * 10 - 5 T |
|||
|
0.775 + 11.7 * 10 -5 T |
|||
|
1.328 + 28.07 * 10 -5 T |
|||
|
0.716 + 7.54 * 10 -5 T |
|||
|
0.628 + 6.75 * 10 -5 T |
Tab. Number 3. Calculation results
The maximum theoretical combustion temperature is found using the heat balance equation :
zhQ H +Q o \u003d Q p.sg.
where: Q o - Heat introduced by the oxidizer;
Qh - Net calorific value of fuel;
g - coefficient of completeness of fuel combustion;
Qn. Cr- Heat received by combustion products;
We find the heat released during the combustion of fuel (lQ h).
From table 2, the value of Q h is taken:
Q h \u003d 27100 kJ / kg
From table 1, the value of w is taken (in my version, w = 0.9)
and*Q H \u003d 0.9 * 27100 \u003d 24390 kJ / kg
Find the heat contributed by the oxidizing agent:
Q o \u003d C p. air *m air* T 1
We determine the average isochoric mass heat capacity of air according to the formula given in table No. 2
c v air \u003d 0.691 + 7.1 * 10 -5 * 660 \u003d 0.73786 kJ / kg * K
We calculate the average isobaric mass heat capacity using the Mayer formula:
Av air \u003d c v air +R \u003d 0.73786 + 0.287 \u003d 1.02486 kJ / kg * K
We determine the theoretically required mass of air:
m o air \u003d 2.67 * C p + 8H p - O p / 0.23 \u003d (2.67 * 0.52 + 8 * 0.13-0.35) / 0.23 \u003d (1.3884 + 1 .04-0.35)/0.23=2.0784/0.23=9.0365 Kg/Kg
Determine the actual mass of air:
m air \u003d a * m o air \u003d 1.0 * 9.0365 \u003d 9.0365 Kg / Kg
Define Q o:
Q o \u003d C p. air * m air * T 1 \u003d 1.02486 * 9.0365 * 660 \u003d 6112.36 kJ / kg
We calculate the heat introduced by the oxidizer and the burnt fuel:
zhQ H +Q o \u003d 24390 + 6112.36 \u003d 30502.36 kJ / kg
We find the heat of combustion products (Qn.Сг):
Q n . Cr \u003d C R, p. sg * m p, sg * T 2.
a) Determine the mass of combustion products:
m p, sg \u003d 1 + m air \u003d 1 + 9.0365 \u003d 10.0365
b) We calculate the mass fractions of the components in the combustion products:
g co 2 \u003d m co 2 / m p, sg \u003d 3.67 * C P / m p, sg \u003d 3.67 * 0.52 / 10.0365 \u003d 0.1901
g H 2 o \u003d m H 2 o / m p, sg \u003d 9 * H p / m p, sg \u003d 9 * 0.13 / 10.0365 \u003d 0.1166
g o2 \u003d m o2 / m p, sg \u003d 0.23 * (a-1) * m o air / m p, sg \u003d 0.23 * (1.0-1) * 9.0365 / 10.0365 \u003d 0
g N2 \u003d m N2 / m p, sg \u003d 0.77 * a * m o air / m p, sg \u003d 0.77 * 1.0 * 9.0365 / 10.0365 \u003d \u003d 0.693
c) Find the average isobaric mass heat capacity of the combustion products using the formula:
C P, p. sg \u003d g (co 2) * C p (co 2) + g (H 2 o) * C p (H 2 O) + g (o 2) * C p (O 2) + g ( N 2) * C p (N 2) \u003d
We find the isobaric heat capacities of the components of the combustion products:
a) c v (co 2) \u003d 0.775 + 11.7 * 10 -5 * T 2
b) c v (H2 o) \u003d 1.328 + 28.07 * 10 -5 * T 2
c) c v (O 2) \u003d 0.628 + 6.75 * 10 -5 * T 2
d) c v (N 2) \u003d 0.716 + 7.54 * 10 -5 * T 2
Using Mayer's formula, we find with p. :
1. C p (co 2) \u003d c v (co 2) + R \u003d 0.775 + 11.7 * 10 -5 * T 2 +0.189 \u003d 0.964 + 11.7 * 10 -5 * T 2
2. C p (H2O) \u003d c v (H2 o) + R \u003d 1.328 + 28.07 * 10 -5 * T 2 +0.462 \u003d 1.79 + 28.07 * 10 -5 * T 2
3. C p (O 2) \u003d c v (O 2) + R \u003d 0.628 + 6.75 * 10 -5 * T 2 + 0.260 \u003d 0.888 + 6.75 * 10 -5 * T 2
4. C p (N 2) \u003d c v (N 2) + R \u003d 0.716 + 7.54 * 10 -5 * T 2 + 0.297 \u003d 1.013 + 7.54 * 10 -5 * T 2
Thus, we find the average isobaric mass heat capacity of the combustion products according to the formula:
C P, p. sg \u003d g (co 2) * C p (co 2) + g (H 2 o) * C p (H 2 O) + g (o 2) * C p (O 2) + g ( N 2) * C p (N 2) \u003d 0.1901 * (0.964 + 11.7 * 10 -5 * T 2) + 0.1166 * (1.79 + 28.07 * 10 -5 * T 2) + 0 * (0.888 + 6.75 * 10 - 5 * T 2) + 0.693 * (1.013 + 7.54 * 10 -5 * T 2) \u003d 0.1832 + 2.2242 * 10 -5 * T 2 + 0.2087 + 3.2729 * 10 -5 * T 2 +0 + 0.702 + 5.2252 * 10 -5 * T 2 = 1.0939 + 10.7223 * 10 -5 * T 2 = 1.0939 + 10.7223 * 10 -5 * 3934.89 = = 1.516
Find the heat of combustion products Q n . SG:
Q n . Cr \u003d C R, p.sg * m p, sg * T 2 \u003d (1.0939 + 10.7223 * 10 -5 * T 2) * 10.0365 * T 2
Using the heat balance equation, we determine the maximum theoretical combustion temperature (T 2):
andQ h= Q n . SG
24390=(1.0939+10.7223*10 -5 *T 2) *10.0365*T 2 we cut both sides by 10.0365:
10.7223*10 -5 *(T 2) 2 +1.09369*T 2 - 2430.13=0
1.09369 + 1.495/0.000214=1875 K
Hosted on Allbest.ru
Similar Documents
Determination of mass, volume and molar heat capacity of a gas mixture. Calculation of the convective heat transfer coefficient and convective heat flow from the pipe to the air in the garage. Calculation according to the formula D.I. Mendeleev of the lowest and highest calorific value of fuel.
test, added 01/11/2015
Gas mixtures, heat capacity. Calculation of the average molar and specific heat capacity. Basic engine cycles internal combustion. Thermal coefficient useful action diesel cycle. Water vapor, steam power plants. General concept of the Rankine cycle.
term paper, added 11/01/2012
Specific heat- the ratio of heat received by a unit amount of a substance to a change in temperature. The dependence of the amount of heat on the nature of the process, and the heat capacity - on the conditions of its course. Thermodynamic processes with an ideal gas.
abstract, added 01/25/2009
Determination of the calorific value for gaseous fuels as the sum of the products of the thermal effects of the components of combustible gases by their quantity. Theoretically required air flow for burning natural gas. Determination of the volume of combustion products.
test, added 11/17/2010
Molar mass and mass heat capacities of the gas mixture. Adiabatic state process. Parameters of the working body at the points of the cycle. Influence of compression ratio, pressure increase and isobaric expansion on the thermal efficiency of a cycle. The process of heat removal along the isochore.
term paper, added 03/07/2010
Determination of air flow and the amount of combustion products. Calculation of the composition of coal dust and the coefficient of excess air during sintering of bauxite in rotary kilns. Using the semi-empirical formula of Mendeleev to calculate the heat of combustion of fuel.
test, added 02/20/2014
Method for calculating the combustion of fuel in air: determining the amount of oxygen in the air, combustion products, calorific value fuel, calorimetric and actual combustion temperature. Combustion of fuel in air enriched with oxygen.
term paper, added 12/08/2011
Thermodynamics as a branch of physics that studies the processes of converting heat into work and other types of energy. Characterization of the key features of the gas thermometer circuit. Consideration of the basic properties of an ideal gas. The essence of the concept of "heat capacity".
presentation, added 04/15/2014
Description of the boiler unit before switching to another type of fuel. Characteristics of burners accepted for installation. Exhaust gas temperature justification. Calculation of the volumes of air and combustion products during the combustion of two types of fuel. Heat balance and fuel consumption.
thesis, added 06/13/2015
Purpose of tunnel dryers. Composition of fuel and calculation of air for combustion. Determination of the total volume of combustion products during fuel combustion and theoretical temperature. Technological calculation of the drying tunnel. Thermotechnical calculation of the drying process.

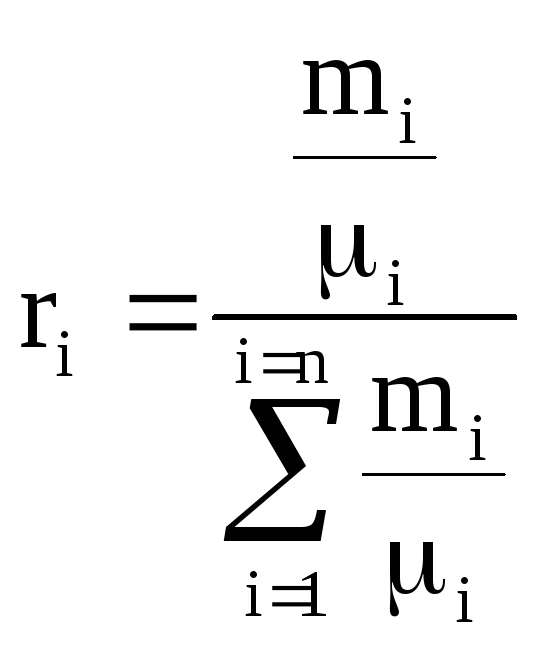
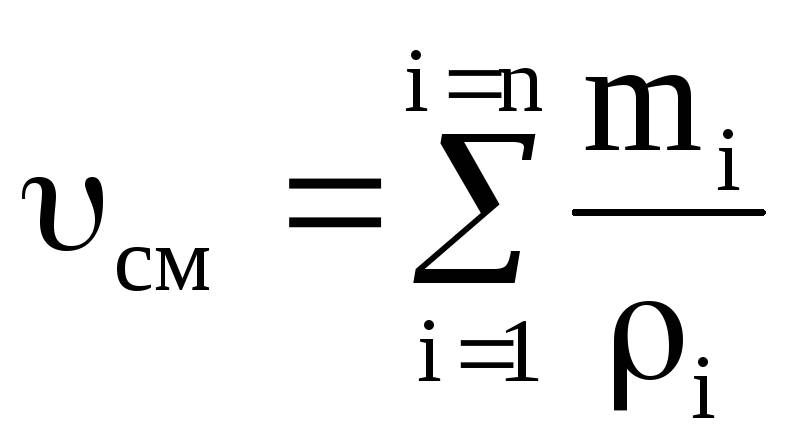
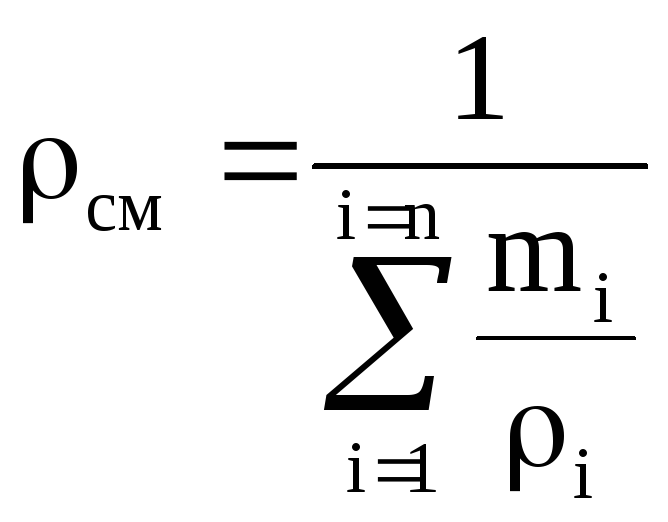
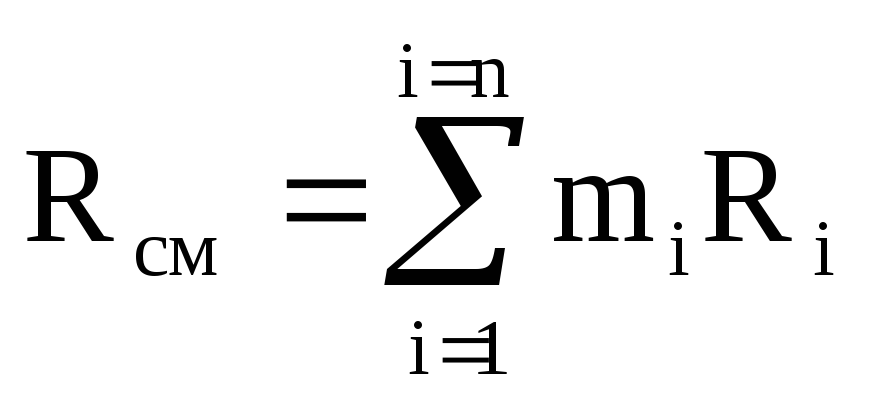

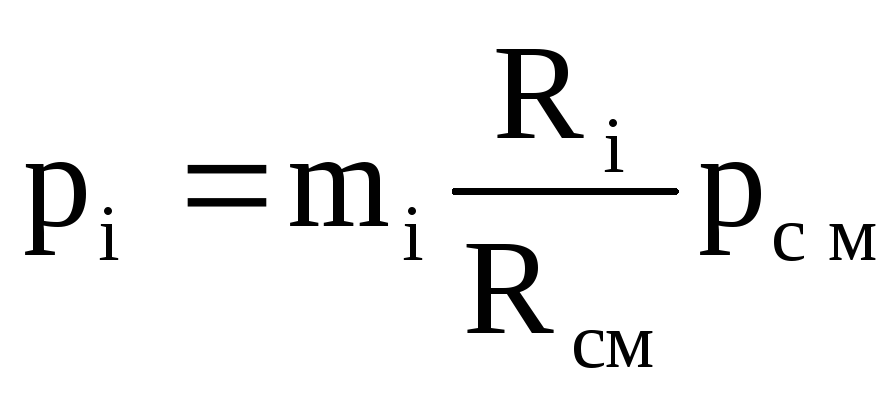
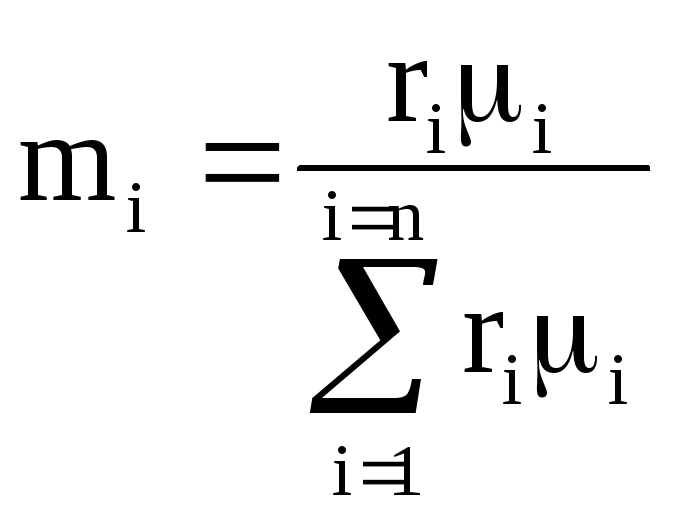
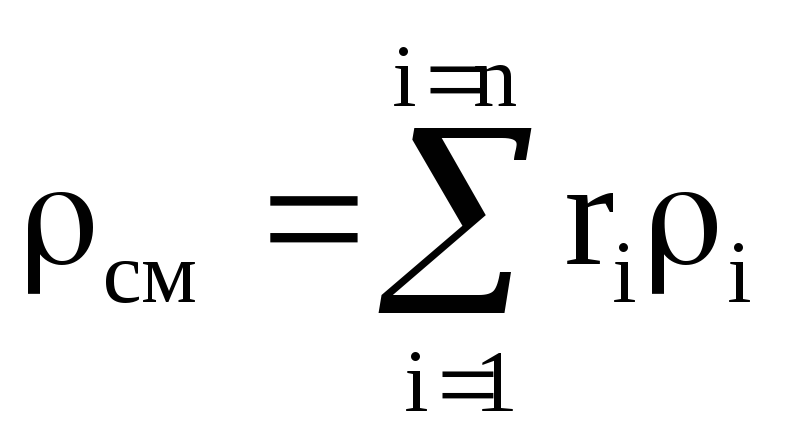
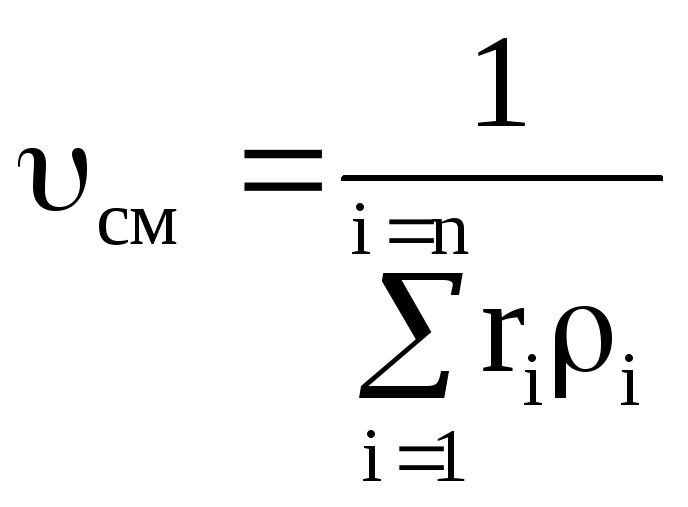
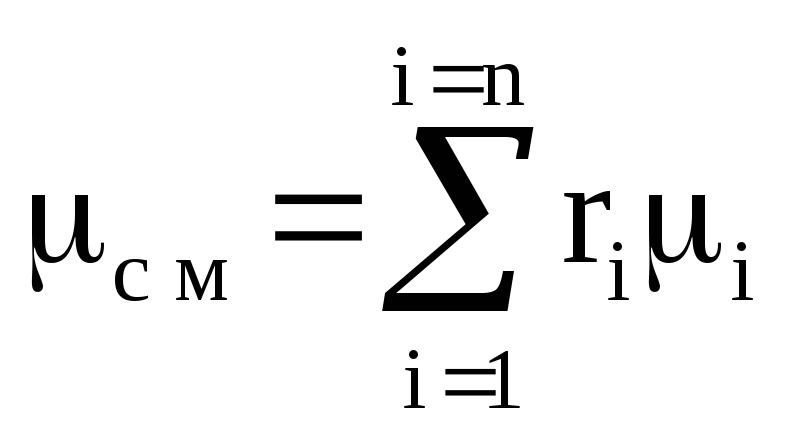
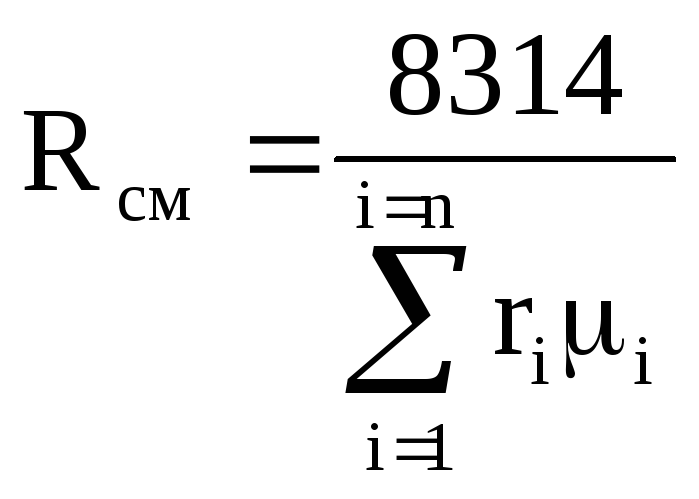
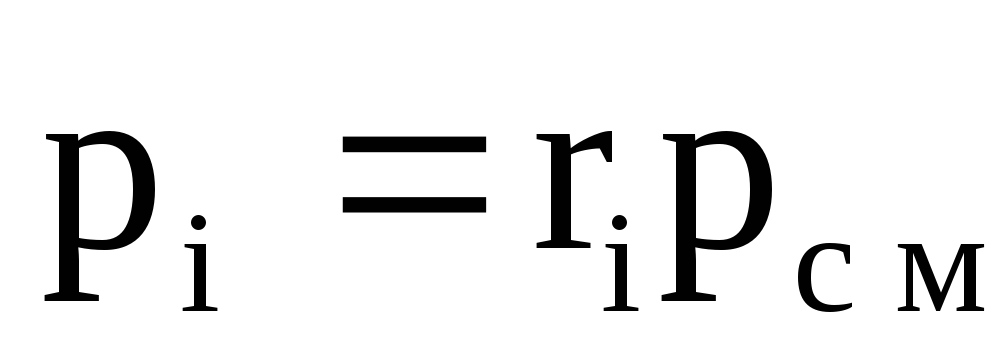
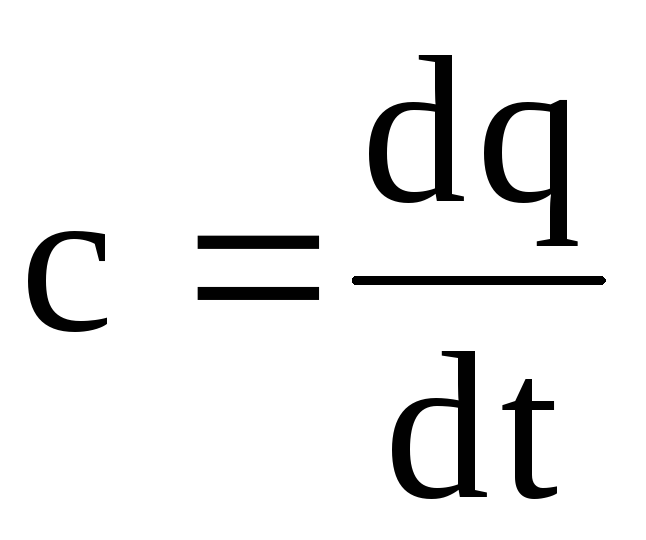 .
(1.28)
.
(1.28)