Ideal gas. Molecular-kinetic theory of ideal gases
Molecular kinetic theory describes the behavior and properties of a special ideal object called ideal gas. This physical model is based on the molecular structure of matter. The creation of molecular theory is associated with the works of R. Clausius, J. Maxwell, D. Joule and L. Boltzmann.
Ideal gas. Molecular-kinetic theory of ideal gas is built on the following assumptions:
atoms and molecules can be seen as material points, which are in continuous motion;
the intrinsic volume of gas molecules is negligible compared to the volume of the vessel;
all atoms and molecules are distinguishable, that is, it is possible in principle to follow the movement of each particle;
before the collision of gas molecules between them, there are no interaction forces, and the collisions of molecules between themselves and with the walls of the vessel are assumed to be absolutely elastic;
the motion of each atom or molecule of a gas is described by the laws of classical mechanics.
The laws obtained for an ideal gas can be used in the study of real gases. For this, experimental models of an ideal gas are created, in which the properties of a real gas are close to those of an ideal gas (for example, at low pressures and high temperatures).
Ideal gas laws
Boyle-Mariotte law:
for a given mass of gas at a constant temperature, the product of the gas pressure and its volume is a constant value: pV = const , (1.1)
at T = const , m = const .
Curve showing the relationship between quantities R and V, characterizes the properties of a substance at a constant temperature, and is called isotherm this is a hyperbola (Fig. 1.1.), and the process proceeding at a constant temperature is called isothermal.
Gay-Lussac's laws:
The volume of a given mass of gas at constant pressure varies linearly with temperature
V = V 0 (1 + t ) at P = const , m = const . (1.2)

p = p 0 (1 + t ) at V = const , m = const . (1.3)
In equations (1.2) and (1.3), temperature is expressed on the Celsius scale, pressure and volume - at
0 С, while
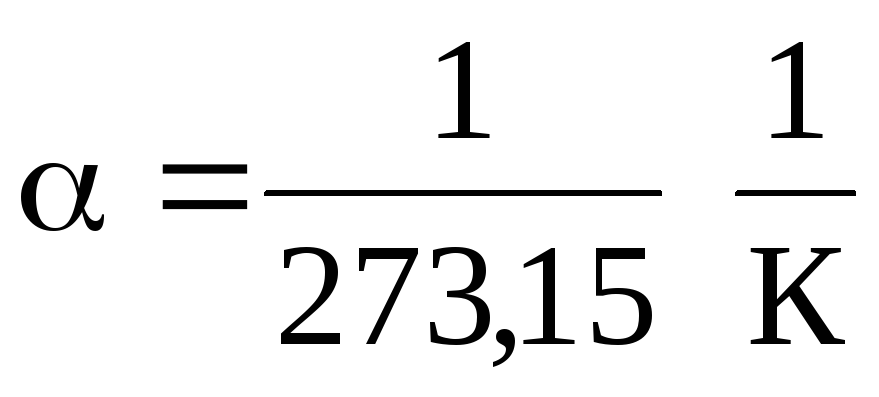 .
.
A process that takes place at constant pressure is called isobaric, it can be represented as a linear function (Fig. 1.2.).
A process that takes place at constant volume is called isochoric(Fig. 1.3.).
It follows from equations (1.2) and (1.3) that isobars and isochores intersect the temperature axis at the point t =1/ \u003d - 273.15 С . If we move the origin to this point, then we move on to the Kelvin scale.
Introducing into formulas (1.2) and (1.3) thermodynamic temperature, the laws of Gay-Lussac can be given a more convenient form:
V = V 0 (1+t) = = V 0 = =V 0 T;
p = p 0 (1+t) = p 0 = p 0 T;
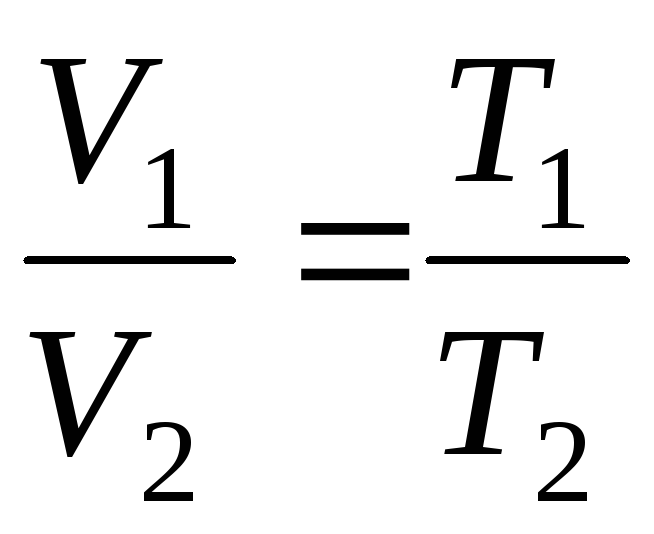 at
p=const, m=const
;
(1.4)
at
p=const, m=const
;
(1.4)
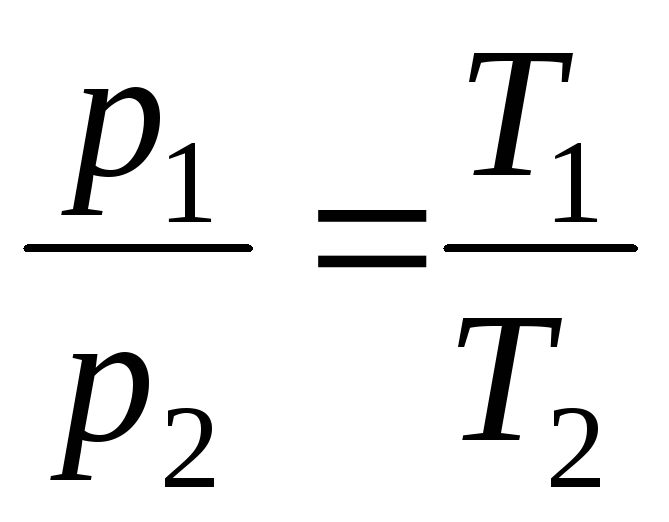 at V = const, m = const
,
(1.5)
at V = const, m = const
,
(1.5)
where indices 1 and 2 refer to arbitrary states lying on the same isobar or isochore .
Avogadro's Law:
moles of any gases at the same temperatures and pressures occupy the same volumes.
Under normal conditions, this volume is equal to V,0 \u003d 22.4110 -3 m 3 / mol . By definition, in one mole various substances contains the same number of molecules, equal to constant Avogadro:N A = 6,02210 23 mol -1 .
Dalton's Law:
mixture pressure ideal gases equal to the sum of the partial pressures R 1 , R 2 , R 3 … R n, gases included in it:
p = p 1 + p 2 + R 3 + …+ p n .
Partial pressure – this is the pressure that the gas in the composition would produce gas mixture if it alone occupied a volume equal to the volume of the mixture at the same temperature.
Ideal gas equation of state
(Clapeyron-Mendeleev equation)
There is a definite relationship between temperature, volume and pressure. This relationship can be represented by a functional dependency:
f(p, V, T)= 0.
In turn, each of the variables ( p, v, t) is a function of two other variables. The type of functional dependence for each phase state of a substance (solid, liquid, gaseous) is found experimentally. This is a very laborious process and the equation of state has been established only for gases that are in a rarefied state, and in an approximate form for some compressed gases. For substances that are not in a gaseous state, this problem has not yet been solved.
The French physicist B. Clapeyron brought ideal gas equation of state, by combining the laws of Boyle-Mariotte, Gay-Lussac, Charles:
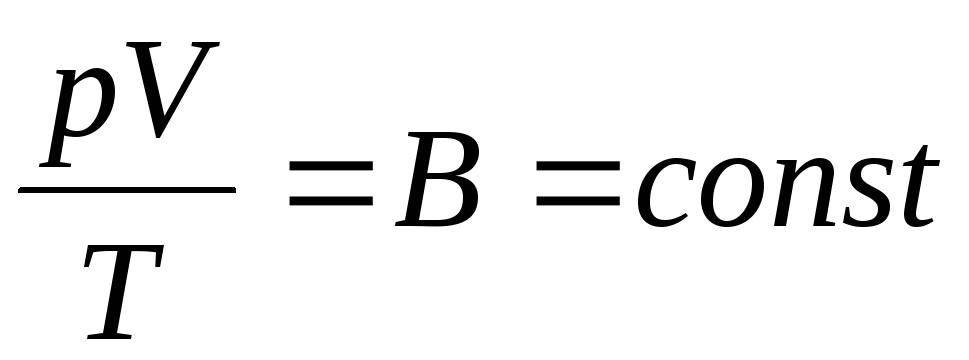 . (1.6)
. (1.6)
Expression (1.6) is the Clapeyron equation, where AT is the gas constant. It is different for different gases.
DI. Mendeleev combined Clapeyron's equation with Avogadro's law, referring equation (1.6) to one mole and using the molar volume V . According to Avogadro's law, for the same R and T moles of all gases occupy the same molar volume V .
.
Therefore, the constant AT will be the same for all ideal gases. This constant is usually denoted R and equal to R=
8,31
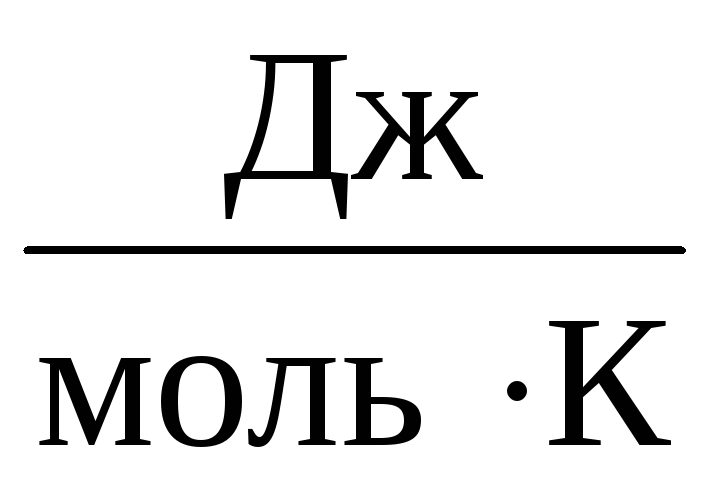 .
.
Clapeyron-Mendeleev equation has the following form:
p V . = R T.
From equation (1.7) for one mole of gas, one can go to to the Clapeyron-Mendeleev equation for an arbitrary mass of gas:
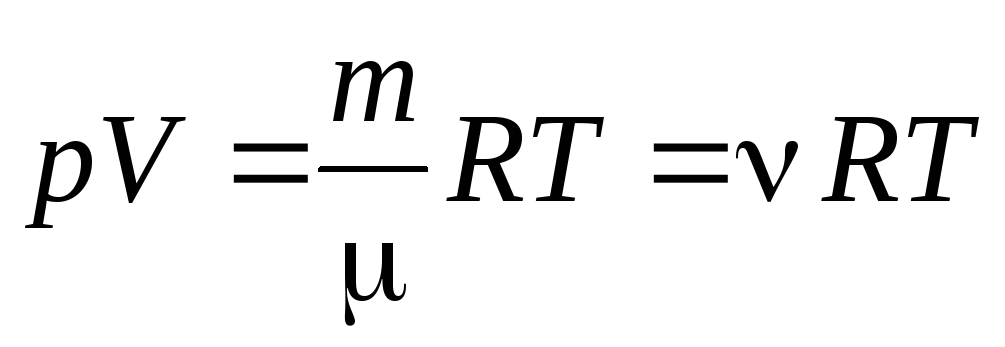 , (1.7)
, (1.7)
where
–
molar mass
(mass of one mole of substance, kg/mol); m
mass of gas;
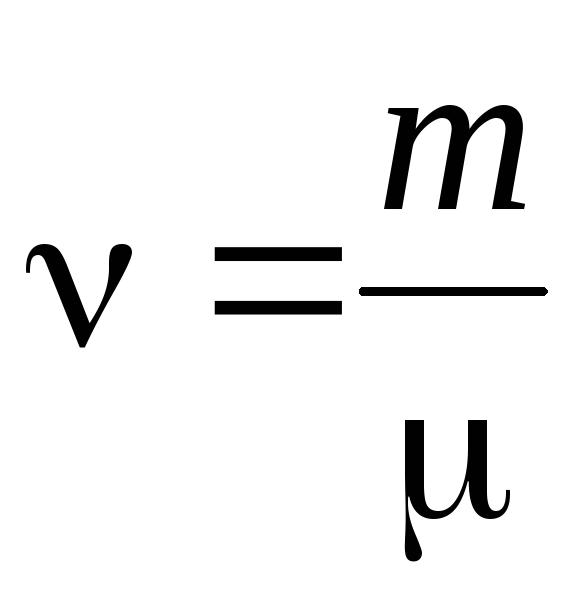 - amount of matter .
- amount of matter .
More often, another form of the ideal gas equation of state is used, introducing Boltzmann's constant: 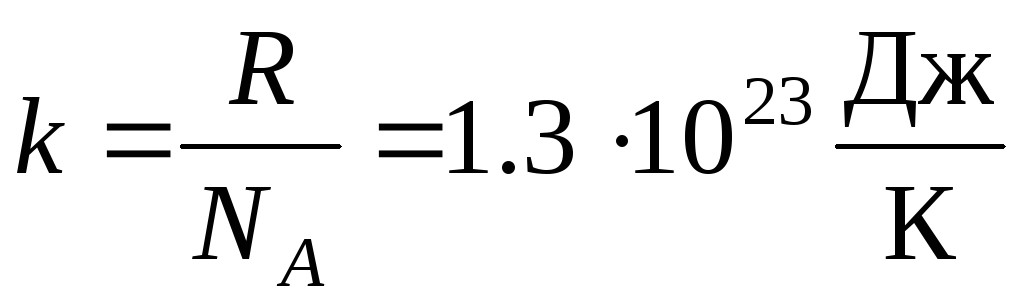 .
.
Then equation (1.7) looks like this:
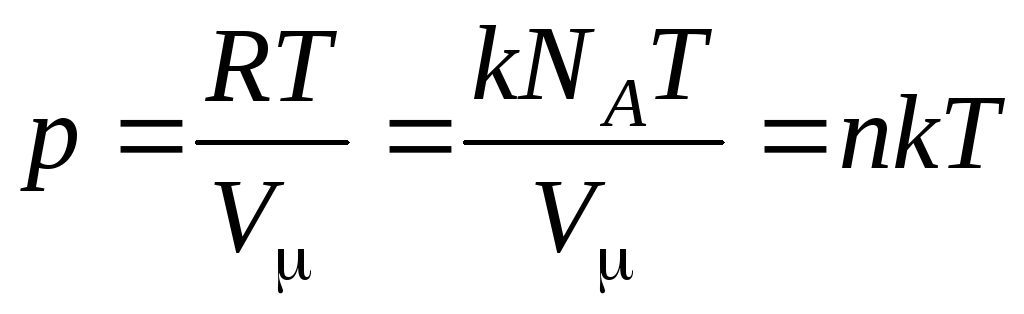 ,
(1.8)
,
(1.8)
where
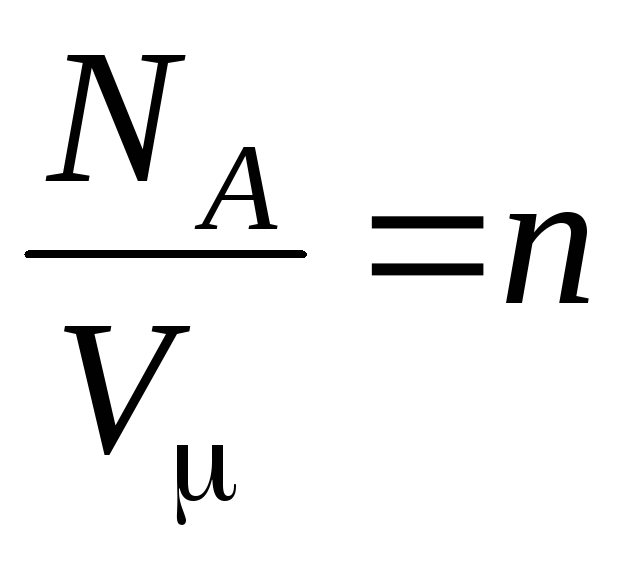 –
concentration of molecules (number of molecules per unit volume). From this expression it follows that the pressure of an ideal gas is directly proportional to the concentration of its molecules or the density of the gas. At the same temperatures and pressures, all gases contain the same number of molecules per unit volume. The number of molecules contained in 1 m 3 under normal conditions is called
Loschmidt number:
–
concentration of molecules (number of molecules per unit volume). From this expression it follows that the pressure of an ideal gas is directly proportional to the concentration of its molecules or the density of the gas. At the same temperatures and pressures, all gases contain the same number of molecules per unit volume. The number of molecules contained in 1 m 3 under normal conditions is called
Loschmidt number:
N L = 2.68 10 25 m -3.
Basic equation of molecular kinetic
theory of ideal gases
The most important task The kinetic theory of gases is the theoretical calculation of the pressure of an ideal gas based on molecular kinetic concepts. The basic equation of the molecular kinetic theory of ideal gases is derived using statistical methods.
It is assumed that the gas molecules move randomly, the number of mutual collisions between the gas molecules is negligible compared to the number of impacts on the walls of the vessel, and these collisions are absolutely elastic. On the wall of the vessel, some elementary area S and calculate the pressure that the gas molecules will exert on this area.
It is necessary to take into account the fact that in reality the molecules can move to the site at different angles and can have various speeds, which, moreover, can change with each collision. In theoretical calculations, the chaotic motions of molecules are idealized, they are replaced by motion along three mutually perpendicular directions.
If we consider a vessel in the form of a cube, in which N gas molecules in six directions, it is easy to see that at any moment 1/3 of the number of all molecules moves along each of them, and half of them (that is, 1/6 of the number of all molecules) moves in one direction, and the second half (also 1/6) - in the opposite direction. With each collision, an individual molecule moving perpendicular to the site, reflecting, transfers momentum to it, while its momentum (momentum) changes by the amount
R 1 =m 0 v – (– m 0 v) = 2 m 0 v.
The number of impacts of molecules moving in a given direction on the site will be equal to: N = 1/6 n Svt. When colliding with the platform, these molecules will transfer momentum to it.
P= N P 1 =2 m 0 vnSvt= m 0 v 2 nSt,
where n is the concentration of molecules. Then the pressure that the gas exerts on the wall of the vessel will be equal to:
p = 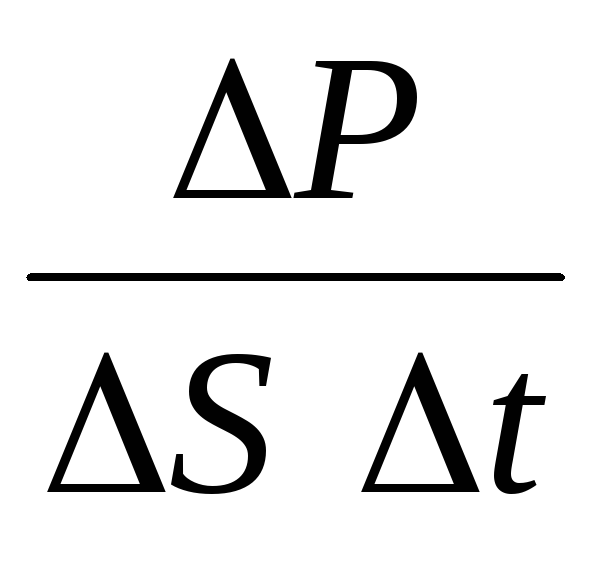 =
n m 0
v 2
.
(1.9)
=
n m 0
v 2
.
(1.9)
However, gas molecules move at different speeds: v 1 , v 2 , …,v n, so the velocities must be averaged. The sum of the squares of the velocities of the gas molecules, divided by their number, determines the root-mean-square velocity:
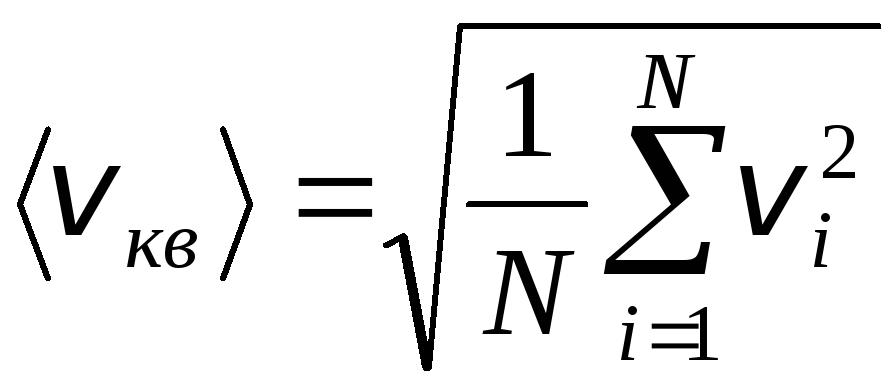 .
.
Equation (1.9) will take the form:
![]() (1.10)
(1.10)
expression (1.10) is called the basic equation of molecular kinetic theory ideal gases.
Given that 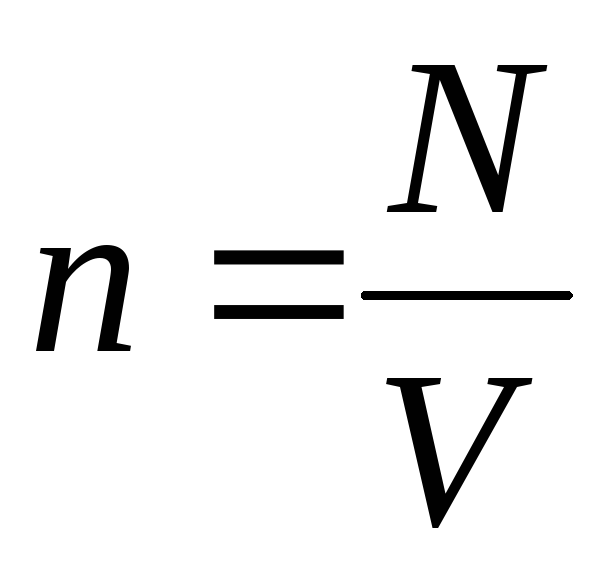 , we get:
, we get:
p V = N 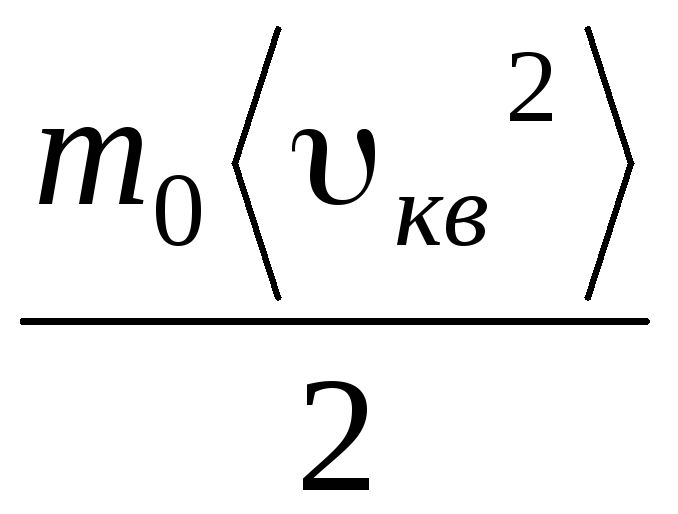 =E,
(1.11)
=E,
(1.11)
where E is the total kinetic energy of the translational motion of all gas molecules. Therefore, the gas pressure is directly proportional to the kinetic energy of the translational motion of the gas molecules.
For one mole of gas m =, and the Clapeyron-Mendeleev equation has the following form:
p V . = R T,
and since it follows from (1.11) that p V . = v sq. 2 , we get:
R.T.= v sq. 2 .
Hence, the root-mean-square velocity of gas molecules is equal to
v
sq.
=
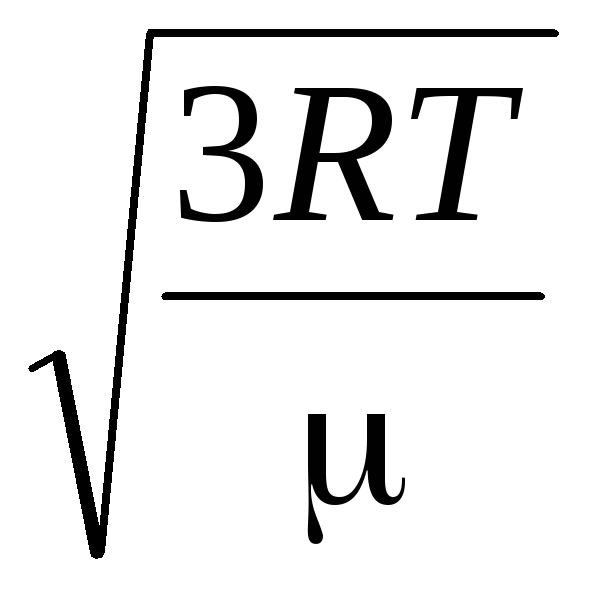 =
=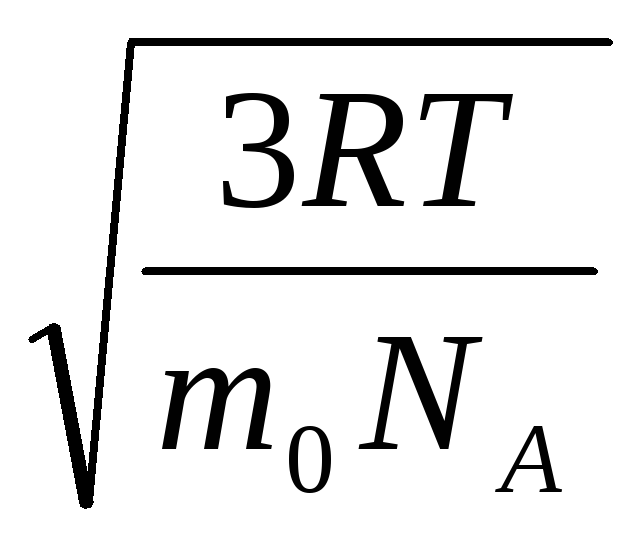 =
= ,
,
where k = R/N A = 1.3810 -23 J/K – Boltzmann's constant. From here you can find the mean square velocity of oxygen molecules at room temperature - 480 m/s, hydrogen - 1900 m/s.
Molecular-kinetic meaning of temperature
Temperature is a quantitative measure of how hot a body is. To clarify the physical meaning of the absolute thermodynamic temperature T Let's compare the basic equation of the molecular-kinetic theory of gases (1.14) with the Clapeyron-Mendeleev equation p V = R.T.
Equating the right parts of these equations, we find the average value of the kinetic energy 0 of one molecule ( = N/N A , k=R/N A):
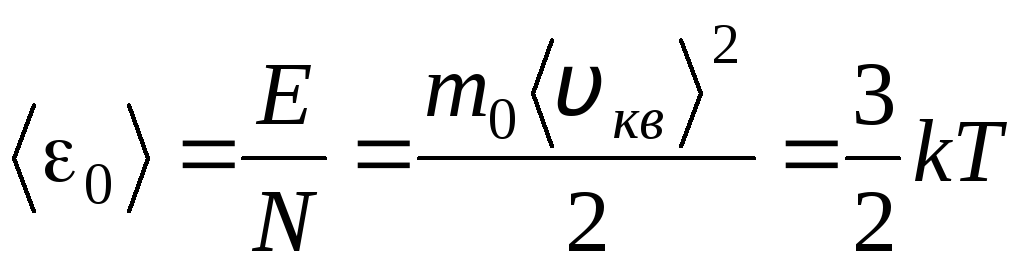 .
.
The most important conclusion of the molecular kinetic theory follows from this equation: the average kinetic energy of the translational motion of one molecule of an ideal gas depends only on temperature, while it is directly proportional to thermodynamic temperature. Thus, the thermodynamic temperature scale acquires a direct physical meaning: at T= 0 the kinetic energy of ideal gas molecules is zero. Therefore, based on this theory, the translational motion of the gas molecules will stop and its pressure will become equal to zero.
Theory of equilibrium properties of an ideal gas
Number of degrees of freedom of molecules. The molecular-kinetic theory of ideal gases leads to a very important consequence: gas molecules move randomly, and the average kinetic energy of the translational motion of the molecule is determined solely by temperature.
The kinetic energy of molecular motion is not exhausted by the kinetic forward motion energy: it also consists of kinetic energies rotation and fluctuations molecules. In order to calculate the energy going into all types of molecular motion, it is necessary to define number of degrees of freedom.
Under number of degrees of freedom (i) of the body is implied the number of independent coordinates that must be entered to determine the position of the body in space.
H  For example, a material point has three degrees of freedom, since its position in space is determined by three coordinates: x, y and z. Therefore, a monatomic molecule has three degrees of freedom of translational motion.
For example, a material point has three degrees of freedom, since its position in space is determined by three coordinates: x, y and z. Therefore, a monatomic molecule has three degrees of freedom of translational motion.
D 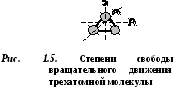 a buchatomic molecule has 5 degrees of freedom (Fig. 1.4): 3 degrees of freedom of translational motion and 2 degrees of freedom of rotational motion.
a buchatomic molecule has 5 degrees of freedom (Fig. 1.4): 3 degrees of freedom of translational motion and 2 degrees of freedom of rotational motion.
Molecules of three or more atoms have 6 degrees of freedom: 3 degrees of freedom of translational motion and 3 degrees of freedom of rotational motion (Fig. 1.5).
Each gas molecule has a certain number of degrees of freedom, three of which correspond to its translational motion.
Regulation on the equal distribution of energy
by degrees of freedom
The basic premise of the molecular-kinetic theory of gases is the assumption of complete randomness in the motion of molecules. This applies to both oscillatory and rotational movements, and not just translational. It is assumed that all directions of motion of molecules in a gas are equally probable. Therefore, it can be assumed that for each degree of freedom of a molecule, on average, there is the same amount of energy - this is the position on the equipartition of energy over degrees of freedom. The energy per one degree of freedom of a molecule is:
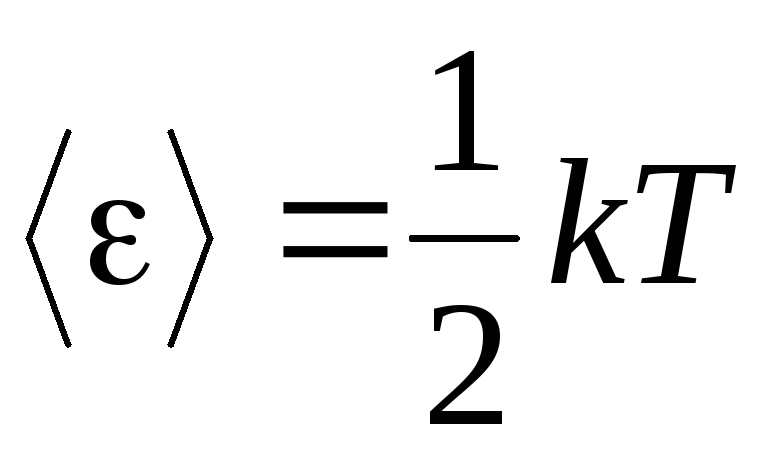 . (1.12)
. (1.12)
If the molecule has i degrees of freedom, then for each degree of freedom there is on average:
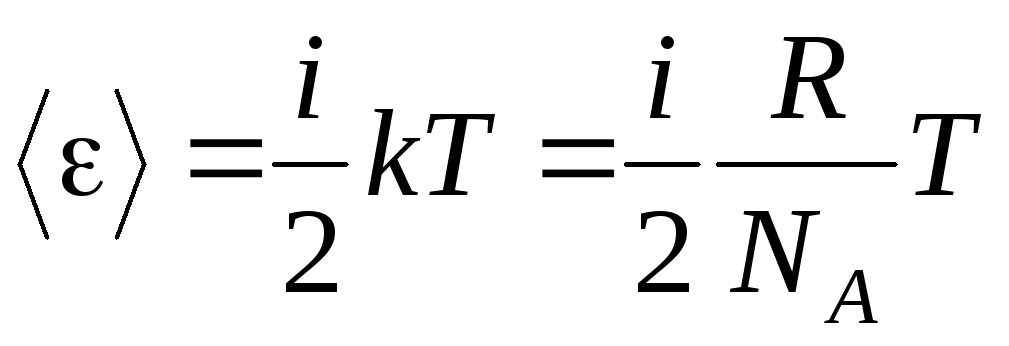 .
(1.13)
.
(1.13)
Internal energy of an ideal gas
If we attribute the total supply of internal energy of the gas to one mole, then we obtain its value by multiplying by the Avogadro number:
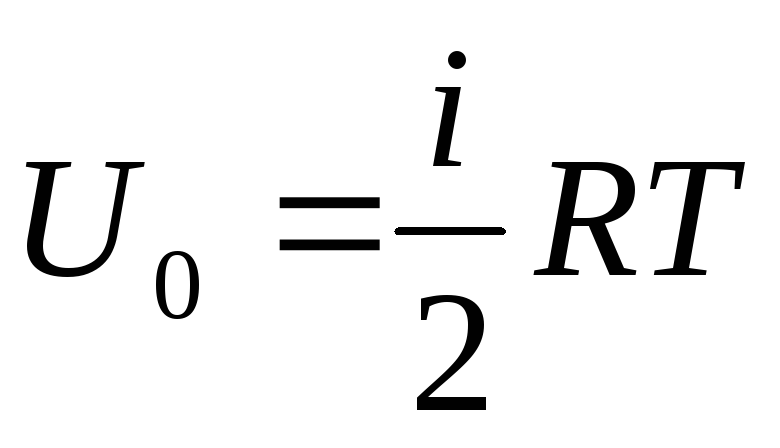 .
(1.14)
.
(1.14)
It follows that the internal energy of one mole of an ideal gas depends only on the temperature and the number of degrees of freedom of the gas molecules.
Maxwell and Boltzmann distributions
Distribution of molecules of an ideal gas in terms of velocities and energies of thermal motion (Maxwell distribution). At a constant gas temperature, all directions of molecular motion are assumed to be equally probable. In this case, the root-mean-square velocity of each molecule remains constant and is equal to
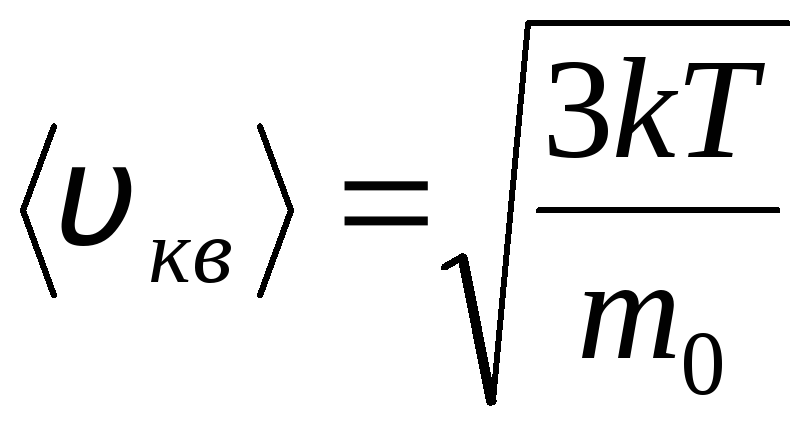 .
.
This is explained by the fact that in an ideal gas, which is in a state of equilibrium, a certain stationary velocity distribution of molecules that does not change with time is established. this distribution is subject to a certain statistical law, which was theoretically derived by J. Maxwell. Maxwell's law is described by the function
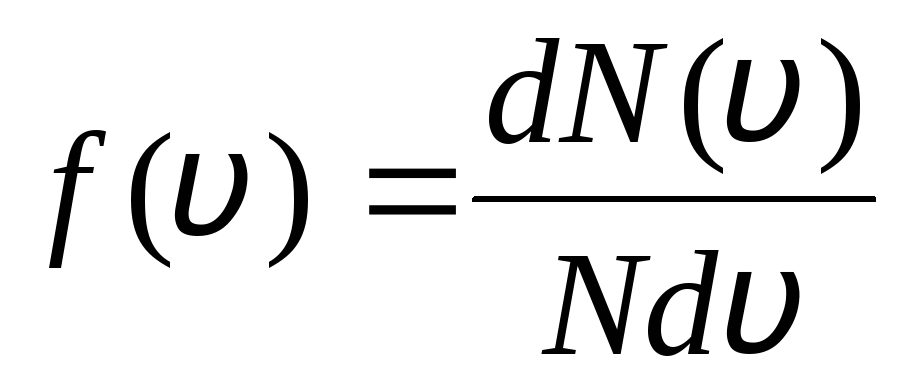 ,
,
that is the function f(v) determines the relative number of molecules  , whose velocities lie in the interval from v
before v+dv. Applying the methods of probability theory, Maxwell found the law of distribution of molecules of an ideal gas in terms of velocities:
, whose velocities lie in the interval from v
before v+dv. Applying the methods of probability theory, Maxwell found the law of distribution of molecules of an ideal gas in terms of velocities:
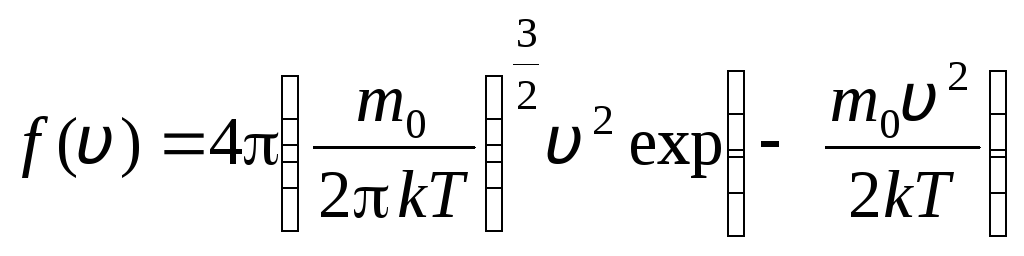 . (1.15)
. (1.15)
The distribution function is shown graphically in fig. 1.6. The area bounded by the distribution curve and the x-axis is equal to one. This means that the function f(v) satisfies the normalization condition:
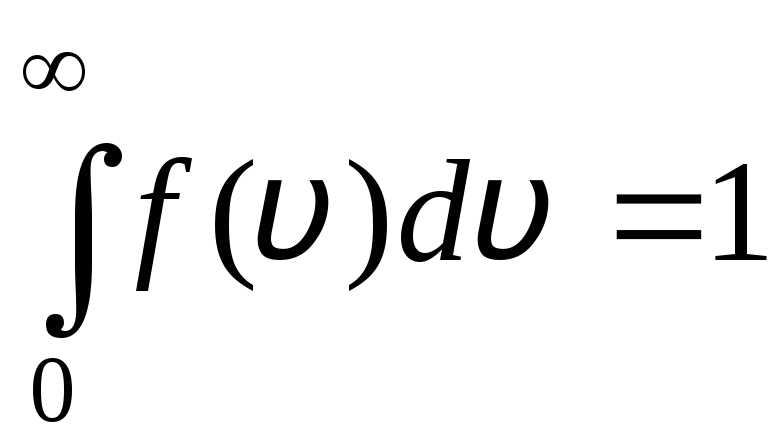 .
.
FROM  velocity at which the distribution function of ideal gas molecules in terms of velocities f(v) is maximum, is called most likely
speed
v B .
velocity at which the distribution function of ideal gas molecules in terms of velocities f(v) is maximum, is called most likely
speed
v B .
Values v = 0 and v = correspond to the minima of expression (1.15). The most probable speed can be found by differentiating expression (1.23) and equating it to zero:
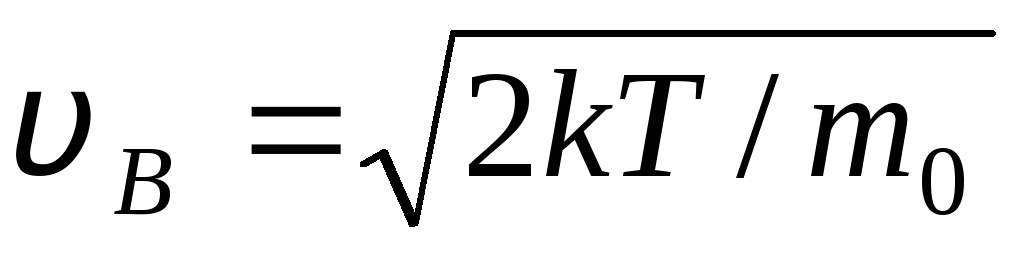 =
=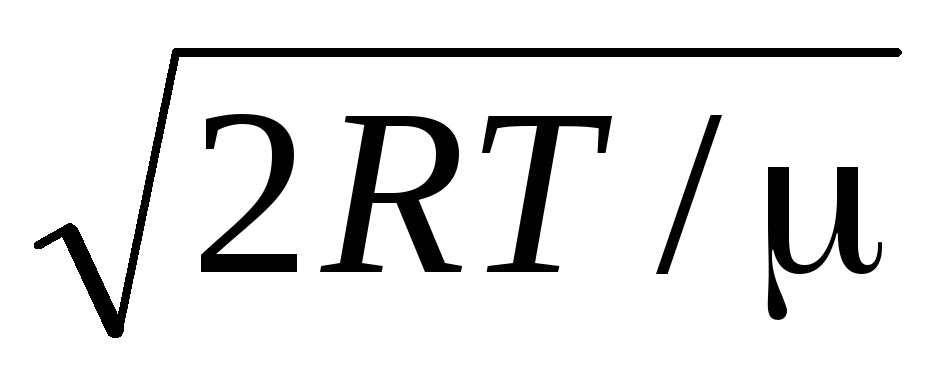 =
1,41
=
1,41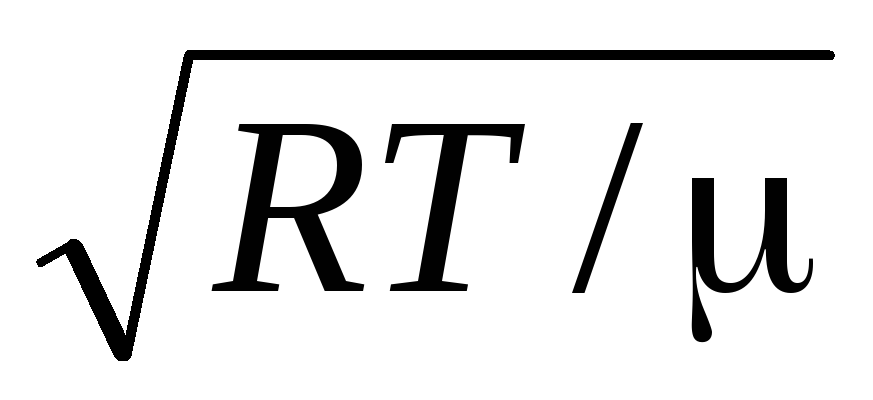
With an increase in temperature, the maximum of the function will shift to the right (Fig. 1.6), that is, with an increase in temperature, the most probable speed also increases, however, the area bounded by the curve remains unchanged. It should be noted that in gases and at low temperatures there is always a small number of molecules that move at high speeds. The presence of such "hot" molecules has great importance during many processes.
Arithmetic average speed molecules is determined by the formula
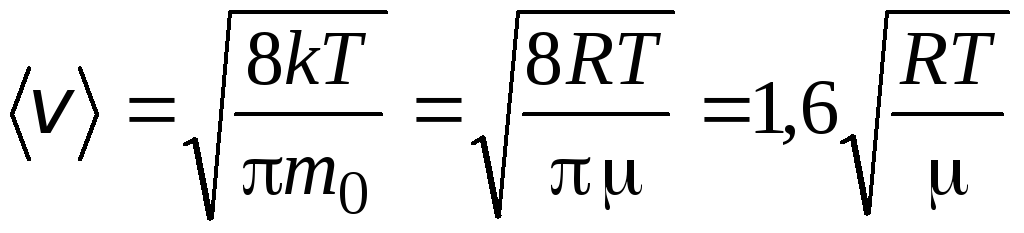 .
.
Root mean square speed
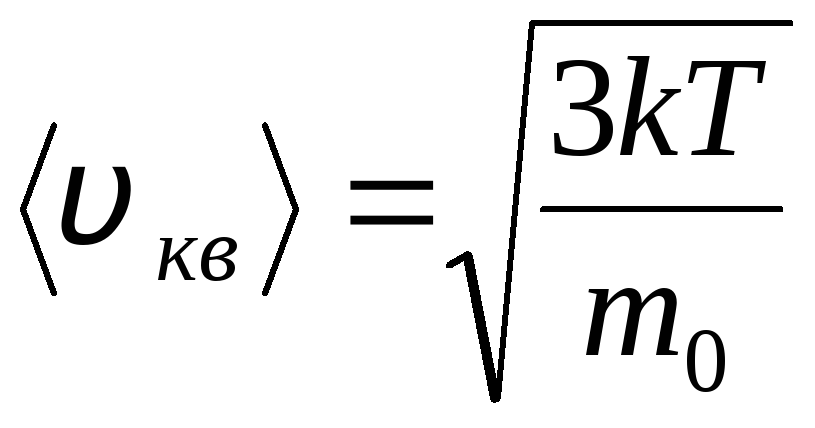 =
1,73
=
1,73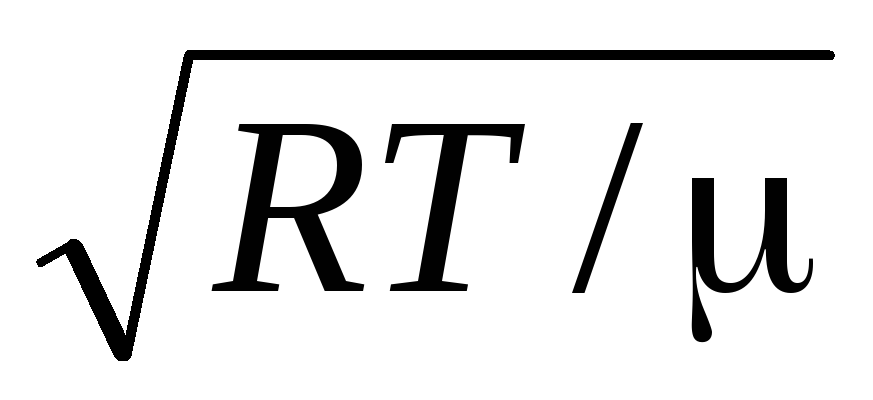 .
.
The ratio of these velocities does not depend on temperature or on the type of gas.
Distribution function of molecules by thermal motion energies. This function can be obtained by substituting the value of kinetic energy instead of velocity into the distribution equation of molecules (1.15):
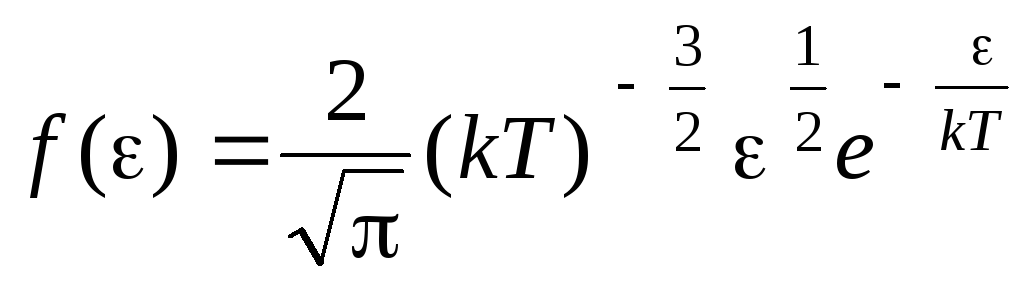 .
.
Having integrated the expression over the energy values from  before
before 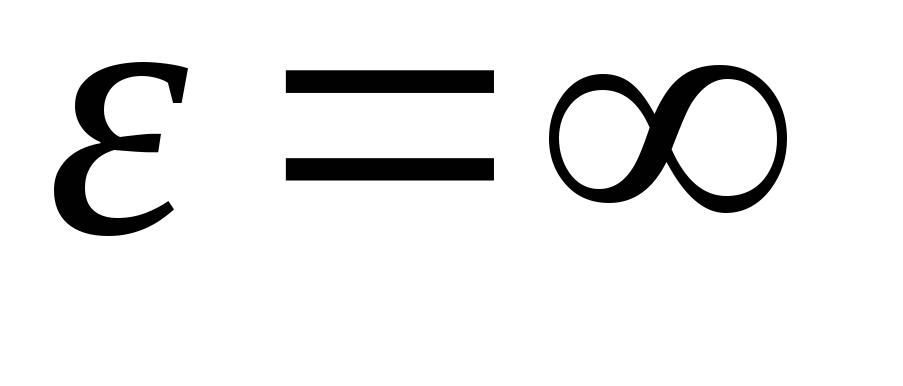
 , we get average kinetic energy ideal gas molecules:
, we get average kinetic energy ideal gas molecules:
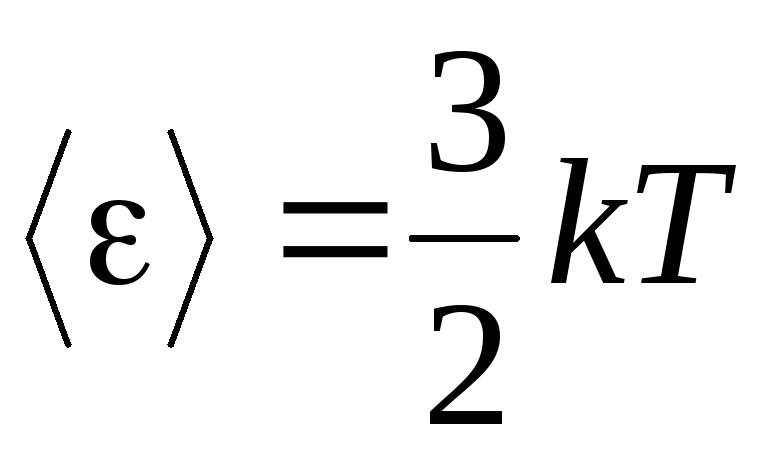 .
.
barometric formula. Boltzmann distribution. When deriving the basic equation of the molecular-kinetic theory of gases and the Maxwell distribution of molecules by velocities, it was assumed that the molecules of an ideal gas are not affected by external forces, therefore the molecules are uniformly distributed throughout the volume. However, the molecules of any gas are in the Earth's gravitational field. When deriving the law of dependence of pressure on height, it is assumed that the gravitational field is uniform, the temperature is constant and the mass of all molecules is the same:
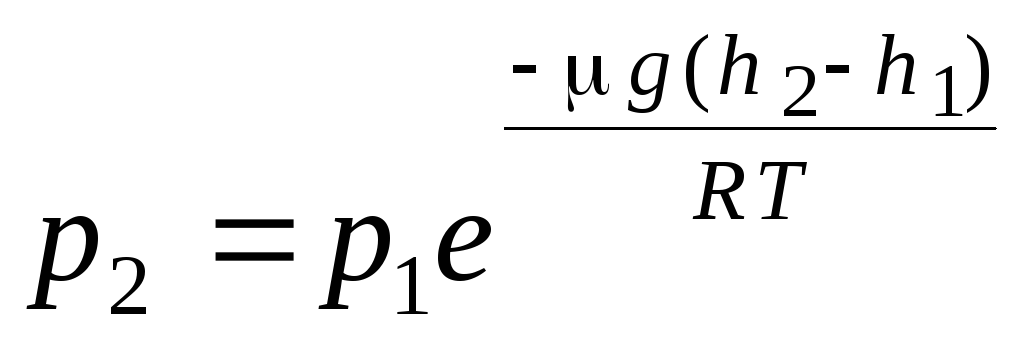 . (1.16)
. (1.16)
Expression (1.16) is called barometric formula. It allows you to find the atmospheric pressure depending on the altitude, or by measuring the pressure, you can find the altitude. Because h 1 is the height above sea level, where the pressure is considered normal, then the expression can be modified:
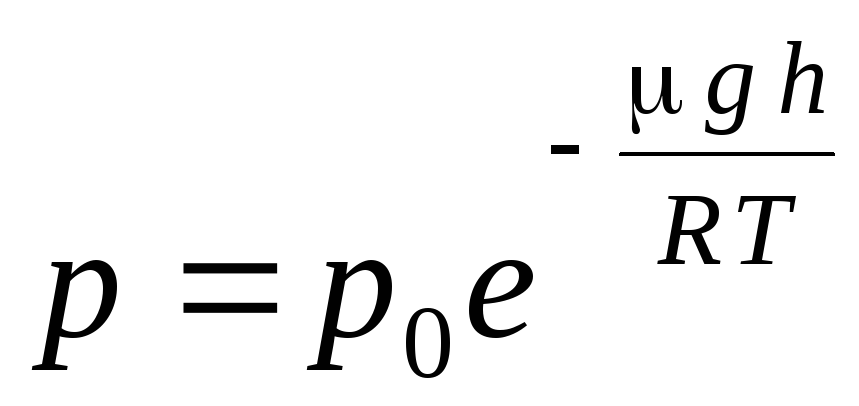 .
.
The barometric formula can be converted using the expression p = nkT:
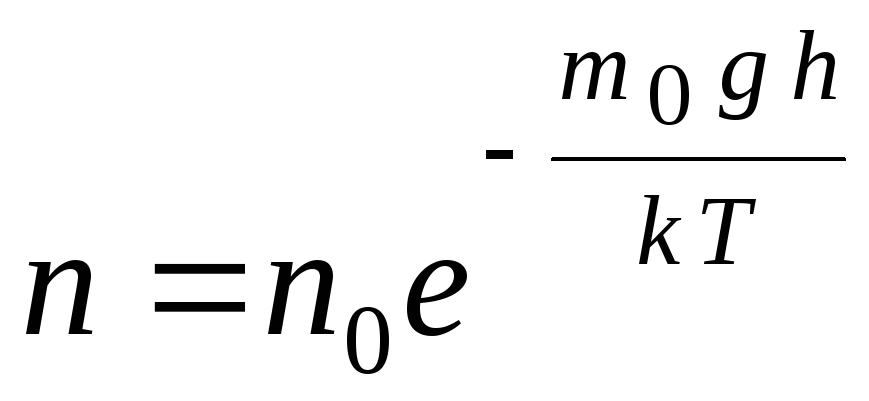 ,
,
G  de n
–
concentration of molecules at altitude h,
m 0
gh=P–
potential energy of a molecule in a gravitational field. At constant temperature, the density of the gas is greater where the potential energy of the molecule is lower. Graphically, the law of decrease in the number of particles per unit volume with height looks as shown in Fig. 1.7.
de n
–
concentration of molecules at altitude h,
m 0
gh=P–
potential energy of a molecule in a gravitational field. At constant temperature, the density of the gas is greater where the potential energy of the molecule is lower. Graphically, the law of decrease in the number of particles per unit volume with height looks as shown in Fig. 1.7.
For an arbitrary external potential field, we write the following general expression
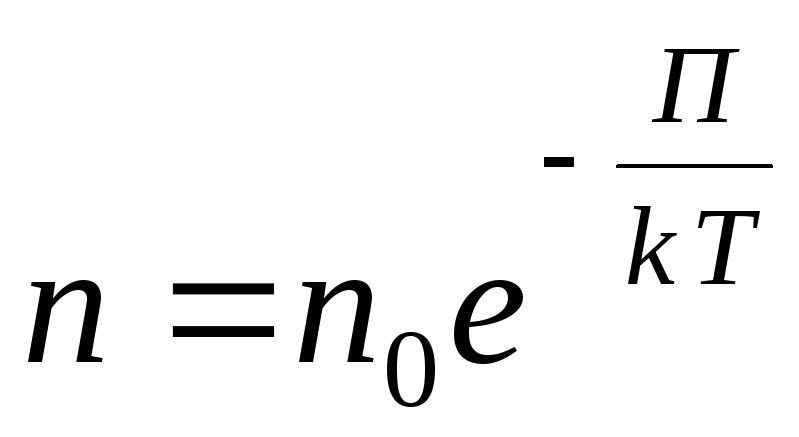 ,
,
In a rarefied gas, the distance between molecules is many times greater than their size. In this case, the interaction between molecules is negligible and the kinetic energy of the molecules is much greater than the potential energy of their interaction.
To explain the properties of a substance in a gaseous state, instead of a real gas, its physical model is used - an ideal gas. The model assumes:
the distance between the molecules is slightly greater than their diameter;
molecules are elastic balls;
there are no attractive forces between molecules;
when molecules collide with each other and with the walls of the vessel, repulsive forces act;
Molecular motion obeys the laws of mechanics.
The basic equation for an ideal gas mkt:
The basic equation of the MKT makes it possible to calculate the pressure of a gas if the mass of the molecule, the average value of the square of the velocity, and the concentration of the molecules are known.
Ideal gas pressure lies in the fact that the molecules in collisions with the walls of the vessel interact with them according to the laws of mechanics as elastic bodies. When a molecule collides with the wall of the vessel, the projection of the velocity v x of the velocity vector on the axis OX, perpendicular to the wall, changes its sign to the opposite, but remains constant in absolute value. Therefore, as a result of collisions of a molecule with a wall, the projection of its momentum on the OX axis changes from mv 1x = -mv x to mv 2x =mv x . A change in the momentum of a molecule upon collision with a wall causes a force F 1 acting on it from the side of the wall. The change in momentum of a molecule is equal to the momentum of this force:
During the collision, according to Newton's third law, the molecule acts on the wall with a force F 2 equal in absolute value to the force F 1 and directed oppositely.
There are many molecules, and each imparts the same momentum to the wall upon collision. In a second they transmit an impulse 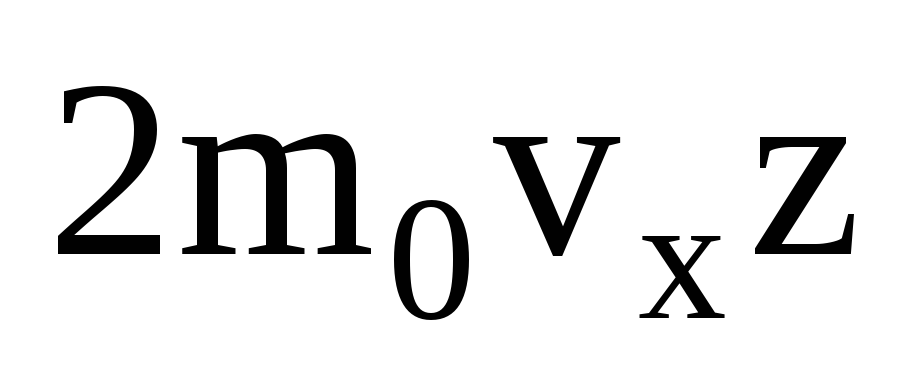 , where z is the number of collisions of all molecules with the wall, which is proportional to the concentration of molecules in the gas, the velocity of the molecules, and the surface area of the wall:
, where z is the number of collisions of all molecules with the wall, which is proportional to the concentration of molecules in the gas, the velocity of the molecules, and the surface area of the wall: 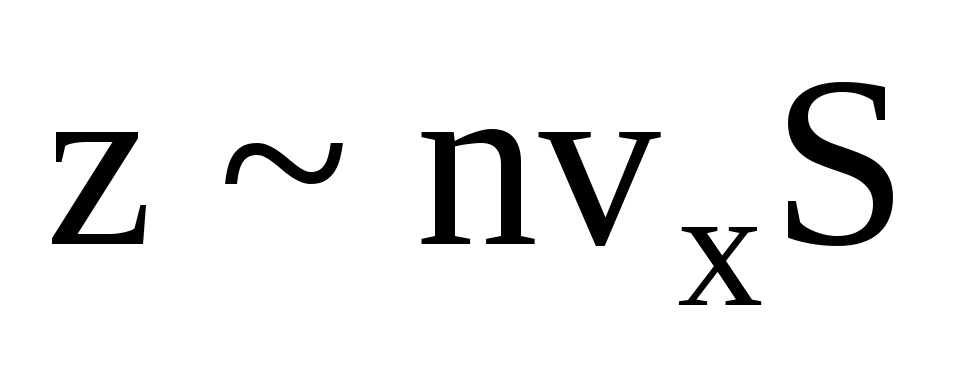 . Only half of the molecules move towards the wall, the rest move in the opposite direction:
. Only half of the molecules move towards the wall, the rest move in the opposite direction: 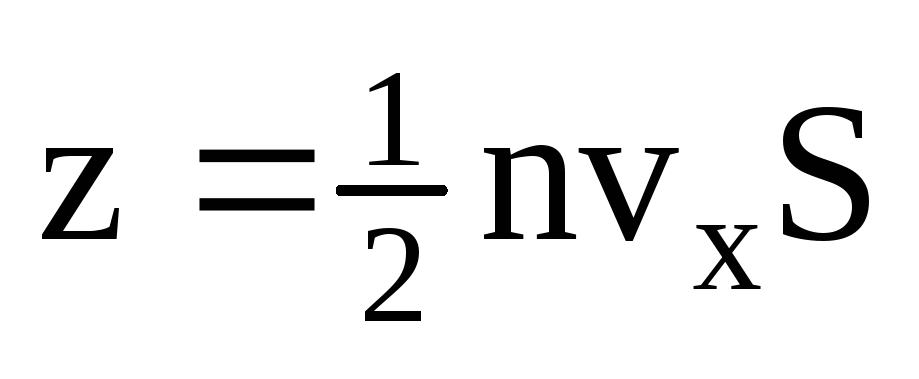 . Then the total momentum transferred to the wall in 1 second:
. Then the total momentum transferred to the wall in 1 second: 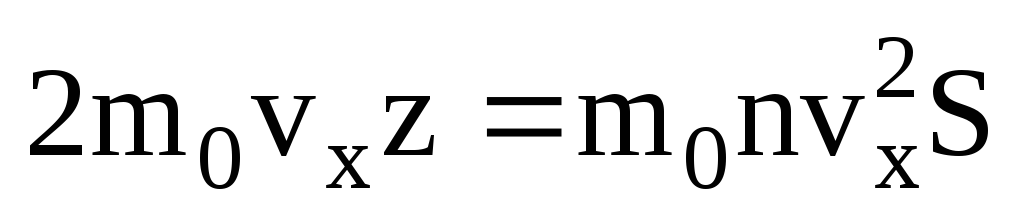 . According to Newton's second law, the change in momentum of a body per unit time is equal to the force acting on it:
. According to Newton's second law, the change in momentum of a body per unit time is equal to the force acting on it:
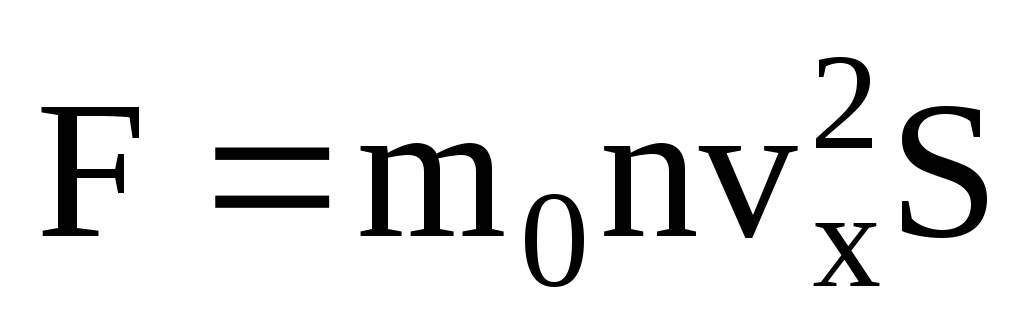
Given that not all molecules have the same speed, the force acting on the wall will be proportional to the mean square of the speed. Since the molecules move in all directions, the average values of the squares of the velocity projections are equal. Therefore, the mean square of the velocity projection is: 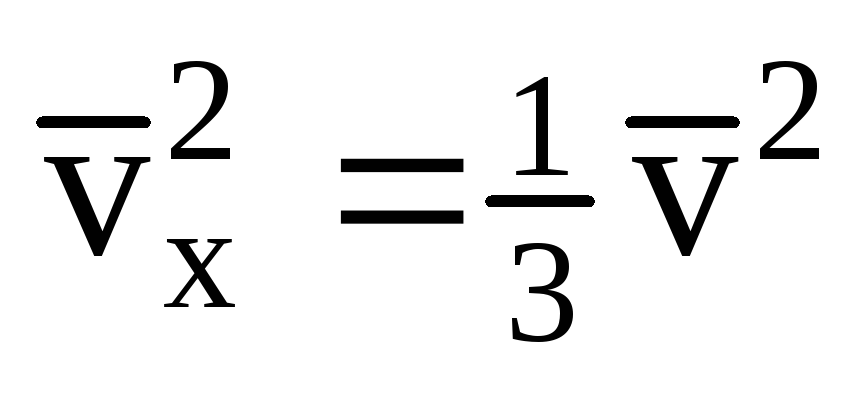 ;
;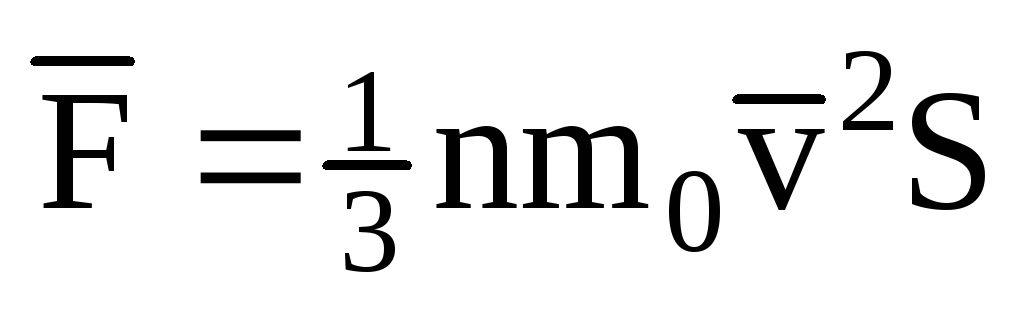 . Then the pressure of the gas on the wall of the vessel is:
. Then the pressure of the gas on the wall of the vessel is:
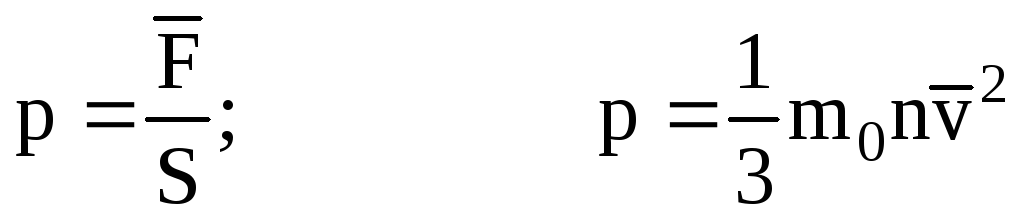 - the basic equation of the MKT.
- the basic equation of the MKT.
Denoting the average value of the kinetic energy of the translational motion of ideal gas molecules:
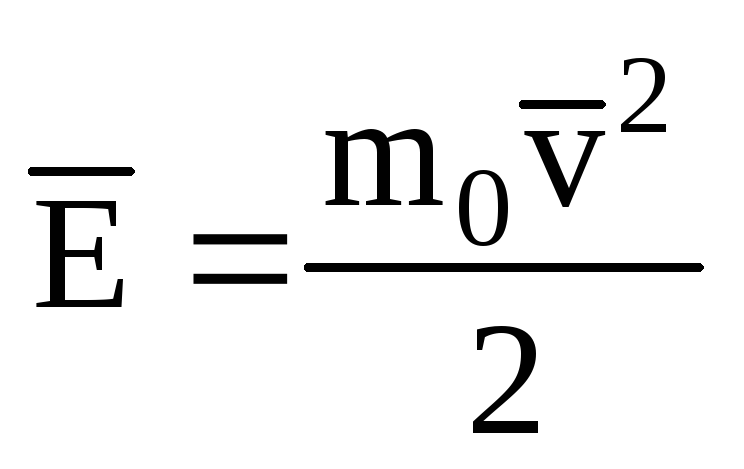 , we get
, we get
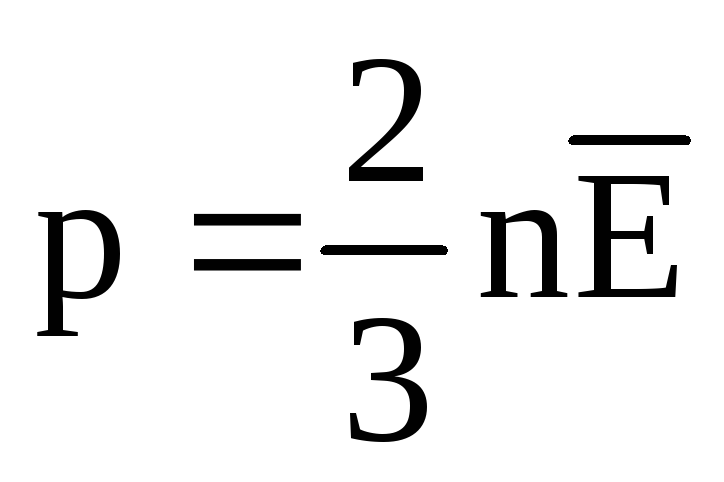
Temperature and its measurement:
The basic MKT equation for an ideal gas relates an easily measurable macroscopic parameter - pressure - to such microscopic gas parameters as the average kinetic energy and concentration of molecules. But, having measured only the pressure, we cannot find out either the average value of the kinetic energy of the molecules separately, or their concentration. Therefore, to find the microscopic parameters of the gas, measurements of some other physical quantity related to the average kinetic energy of the molecules are needed. This value is temperature.
Any macroscopic body or group of macroscopic bodies, under constant external conditions, spontaneously passes into a state of thermal equilibrium. Thermal equilibrium - this is a state in which all macroscopic parameters remain unchanged for an arbitrarily long time.
Temperature characterizes the state of thermal equilibrium of a system of bodies: all bodies of the system that are in thermal equilibrium with each other have the same temperature.
To measure temperature, you can use the change in any macroscopic quantity depending on temperature: volume, pressure, electrical resistance, etc.
Most often in practice, the dependence of the volume of liquid (mercury or alcohol) on temperature is used. When calibrating a thermometer, the temperature of melting ice is usually taken as the reference point (0); the second constant point (100) is the boiling point of water at normal atmospheric pressure (Celsius scale). Since different liquids expand differently when heated, the scale thus established will depend to some extent on the properties of the given liquid. Of course, 0 and 100°C will match for all thermometers, but 50°C will not match.
Unlike liquids, all rarefied gases expand in the same way when heated and change their pressure in the same way with a change in temperature. Therefore, in physics, to establish a rational temperature scale, a change in the pressure of a certain amount of rarefied gas at a constant volume or a change in the volume of a gas at a constant pressure is used. This scale is sometimes called ideal gas temperature scale.
At thermal equilibrium, the average kinetic energy of the translational motion of the molecules of all gases is the same. The pressure is directly proportional to the average kinetic energy of the translational motion of the molecules: 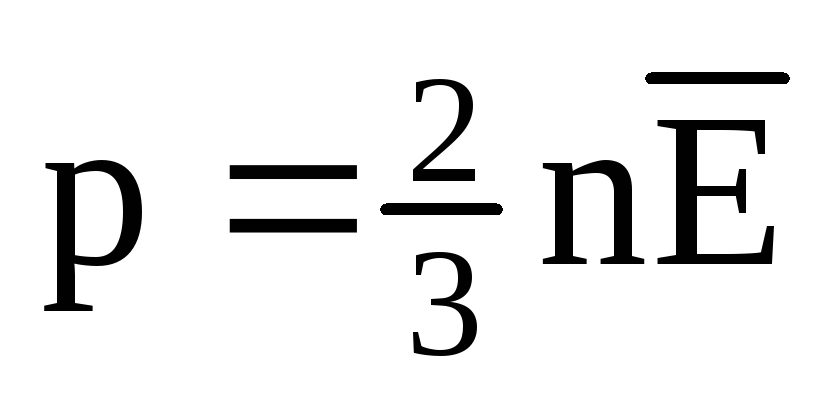 . At thermal equilibrium, if the pressure of a gas of a given mass and its volume are fixed, the average kinetic energy of the gas molecules must have a strictly defined value, like the temperature. Because
. At thermal equilibrium, if the pressure of a gas of a given mass and its volume are fixed, the average kinetic energy of the gas molecules must have a strictly defined value, like the temperature. Because 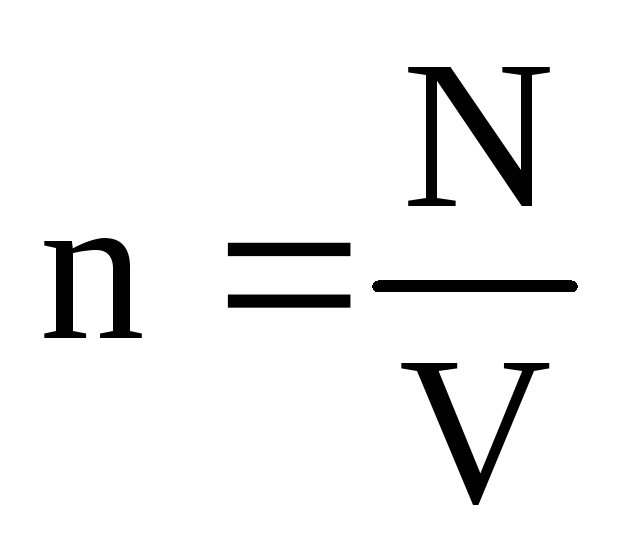 , then
, then 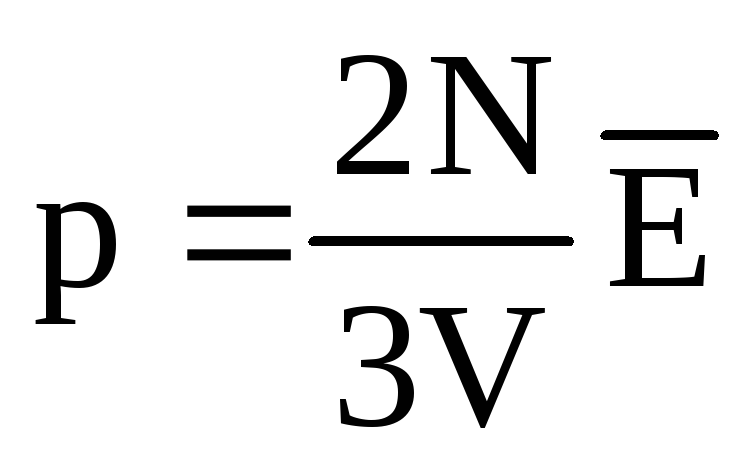 , or
, or 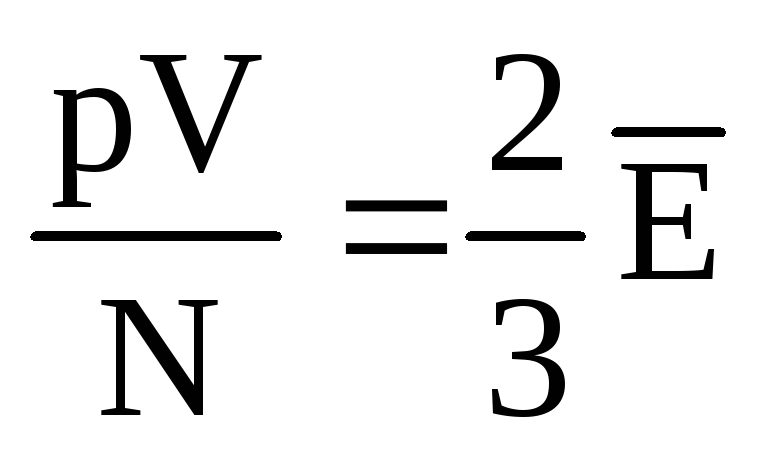 .
.
Denote 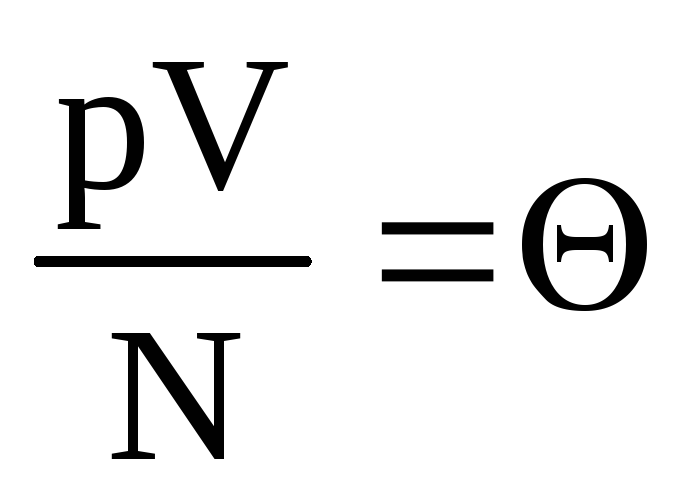 . Value
. Value  increases with temperature and does not depend on anything other than temperature. Therefore, it can be considered a natural measure of temperature.
increases with temperature and does not depend on anything other than temperature. Therefore, it can be considered a natural measure of temperature.
Did you know,
what is a thought experiment, gedanken experiment?
It is a non-existent practice, an otherworldly experience, the imagination of what is not really there. Thought experiments are like daydreams. They give birth to monsters. Unlike a physical experiment, which is an experimental test of hypotheses, a “thought experiment” magically replaces an experimental test with the desired, untested conclusions, manipulating logical constructions that actually violate logic itself by using unproved premises as proven ones, that is, by substitution. Thus, the main task of the applicants of "thought experiments" is to deceive the listener or reader by replacing a real physical experiment with his "doll" - fictitious reasoning on parole without physical verification itself.
Filling physics with imaginary, "thought experiments" has led to an absurd, surreal, confusing picture of the world. A real researcher must distinguish such "wrappers" from real values.
Relativists and positivists argue that the "thought experiment" is a very useful tool for testing theories (also arising in our minds) for consistency. In this they deceive people, since any verification can only be carried out by a source independent of the object of verification. The applicant of the hypothesis himself cannot be a test of his own statement, since the reason for this statement itself is the absence of contradictions visible to the applicant in the statement.
We see this in the example of SRT and GTR, which have turned into a kind of religion that governs science and public opinion. No amount of facts that contradict them can overcome Einstein's formula: "If the fact does not correspond to the theory, change the fact" (In another version, "Does the fact not correspond to the theory? - So much the worse for the fact").
The maximum that a "thought experiment" can claim is only the internal consistency of the hypothesis within the framework of the applicant's own, often by no means true, logic. Compliance with practice does not check this. A real test can only take place in a real physical experiment.
An experiment is an experiment, because it is not a refinement of thought, but a test of thought. Thought that is consistent within itself cannot test itself. This has been proven by Kurt Gödel.
