What is HEAT CAPACITY

When heat is supplied, the temperature of the system rises. In the case of an infinitely small change in temperature, the proportionality is valid

dT=δQ , or dT=constδQ

It is more convenient to write this relation in the form: δQ=СdT or

The value C is called the true heat capacity of the system.

Heat capacity is the ratio of the amount of heat supplied to the system to the temperature change that occurs.

In addition to the true, there is also an average heat capacity:

Heat capacity

If the heat capacity is attributed to a unit mass (mole) of a substance, then it becomes independent of the mass of the entire system and acquires the properties of an intensive parameter. If the heat capacity refers to a unit mass of a substance, it is called specific, and to 1 mole - heat capacity with the dimension of J / (mol * k)

We will consider only molar heat capacities, since for them, all regularities are much simpler than for specific heat capacity.

The heat capacity depends on the conditions under which the transfer of heat to the system takes place. If the system is enclosed in a constant volume, then an increase in temperature by dT will occur under the action of heat equal to CvdT, where Cv is the heat capacity at constant volume. In cases of constant pressure during the expansion of the system, to increase the temperature by dT, heat CpdT will be required, where Cp is the heat capacity at constant pressure.

Given the conditions for the transfer of heat, when one or more variables are kept constant, while others change, the heat capacity can be expressed using partial derivatives: . Since δQ v = dU,

δQ p =dH, we can write:

(1)

Cv is the isochoric heat capacity of gases, Cp is the isobaric heat capacity of gases.

The differences between isochoric and isobaric heat capacities are due to the difference in internal energy and enthalpy. Changes in enthalpy and internal energy differ by the amount of work done by the system.

δW=∆nRT, ∆H-∆U=∆nRT

Therefore, the heat capacities at constant volume Cv and constant pressure Cp also differ by the amount of work: Cp - Cv = δW

Based on expressions (1), we can write:

Substituting these equalities into the equation ∆H- ∆U=∆nRT

and taking into account that ∆n= 1, we will find the relationship between the molar heat capacities of gases:

Cp– Cv= R or Cp= Cv+ R

As can be seen, they differ by the value of the gas constant.

From the condition Cp= Cv+ R it follows that Cp˃Cv, i.e. in an isobaric process, when P=const, to increase the temperature of the system, it is required large quantity heat than in an isochoric process.

The molar heat capacity of gases has values ​​of the order of R, so the difference between Cp and Cv is very significant. So, for carbon dioxide CO 2 at 25 0 C Cp = 37, 14; and Cv = 28.83 J / (mol * K)

The difference Cp - Cv is the work of the isobaric expansion of one mole ideal gas when the temperature rises by one degree. Liquids and solids of the body are characterized by a slight increase in volume when heated. Therefore, for condensed bodies, we can assume that Ср ≈ Сv.

KIRCHHOFF EQUATION. DEPENDENCE OF THERMAL EFFECTS ON TEMPERATURE.

The previously considered calculations of thermal effects based on the Hess law for the heat of formation and combustion are limited by standard conditions. For practical purposes, it is necessary to calculate thermal effects for specific conditions other than standard ones.

Go from known thermal effects under standard conditions, i.e. at a temperature of 25 0 C (298.15 K) and a pressure of 1 atm. (1.013 * 10 5 Pa), it is possible to calculate thermal effects at any temperature of interest to us using Kirchhoff's law. Processes in industrial conditions are characterized by a significant temperature variation, the range of which is determined not only by the conditions of the technology, but also by the season. This range can reach hundreds of degrees - it is natural that the thermal effects will be significantly different and depend on temperature.

Consider Kirchhoff's law in differential form. To do this, we write down the changes in enthalpy in isobaric and internal energy in isochoric processes.

∆H \u003d H 2 -H 1; ∆U \u003d U 2 -U 1.

Differentiate these equations with respect to temperature and obtain:

Kirchhoff equations:

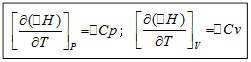
And - temperature coefficients of the thermal effect of isobaric and isochoric processes, respectively; and - change in the heat capacity of the system as a result of isobaric and isochoric processes, respectively.

On the basis of the Kirchhoff equation, the Kirchhoff law is formulated in differential form: the temperature coefficient of the thermal effect of the process is equal to the change in the heat capacity of the system that occurs as a result of this process.

Thus, Kirchhoff's law in differential form makes it possible to determine only the change in the thermal effect with temperature, and not the magnitude of the thermal effect itself.

Let us analyze the Kirchhoff equation

For the reaction: aA + bB = dD + rR in an isobaric process (р=const), according to the Kirchhoff law, the change in heat capacity in the system will have the form:

A similar expression can be obtained for an isochoric process:

Since Kirchhoff's law allows you to determine the changes in the thermal effect of the process with a change in temperature, we build a graph:

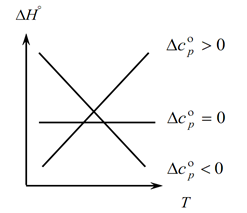
1. Consider the first case, when ∆Ср(∆Сv)˃0, because ∆Ср=∑С con. -∑С initial, hence it follows that the sum of the heat capacities of the reaction products is greater than the sum of the heat capacities of the starting substances: ∑С con. ˃∑From the beginning In this case, we obtain curve 1 on the graph, which means that as the temperature increases, the change in the thermal effect of the process also increases (T and ∆H);

2. The second case, when ∆Ср(∆Сv)˂0. Similarly to the first law, we have ∑С con. ˂∑From early (the sum of the heat capacities of the final products is less than the sum of the heat capacities of the initial substances). Then we get a curve on the graph, which means that with an increase in temperature, the change in the thermal effect of the process decreases (Т→∆H↓)

3. And the third case, when the change in the heat capacities of the system is equal to zero ∆Ср(∆Сv)=0. Then the sum of the heat capacities of the final products of the reactions is equal to the sum of the heat capacities of the starting materials ∑С con. \u003d ∑ From the beginning. In this case, the thermal effect of the reaction is not a function of temperature (∆H ≠ f(T)) and we get a straight line on the graph.

CALCULATION OF THERMAL EFFECTS FOR A GIVEN

TEMPERATURE. INTEGRATION OF THE KIRCHHOFF EQUATION

To find the value of the thermal effect as a function of temperature, it is necessary to integrate the equations

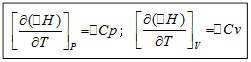
From T to T 0 (where T is the required temperature, T 0 is the standard temperature), from ∆H to ∆H 0 or from ∆U to ∆U 0 (where ∆H and ∆U are the enthalpy and internal energy under conditions that differ from standard). Integration is carried out for two cases:

For not organic matter: For organic substances:

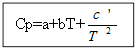
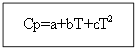
Example: for H 2 (g) - inorganic substance

Ср=f(T)	T
a	b*10 3	c’*10 -5	289-3000
27,28	3,26	0,50

Cp (H 2 (g)) \u003d 27.28 + 3.26 * 10 -3 T +.

a) Approximate integration:

for isobaric process

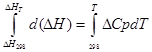
∆H T - ∆H 298 =∆Cp*(T-298)

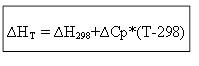
for isochoric process:

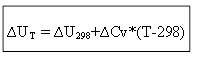
Thus, to determine the thermal effect ∆H or internal energy ∆U at any temperature T, it is necessary to know the heat of the process under standard conditions ∆H 0 (∆U 0) and the change in heat capacities ∆Ср, ∆Cv.

Example. Calculate the thermal effect ∆H of the process of obtaining benzene from acetylene:

3C 2 H 2 (g) → C 6 H 6 (g) at 75 0 C (348K).

1. We find from the tables the average molar isobaric heat capacities of benzene and acetylene:

Ср С6Н6 (g) \u003d 81.67 J / (mol * K);

Cp C2H2 (g) \u003d 43.93 J / (mol * K).

2. We find the change in the heat capacity of the process:

∆Cp \u003d ∑ (nCp) con - ∑ (nCp) initial \u003d Cp C6H6 (g) - 3 * Cp C2H2 (g) \u003d 81.67 - 3 * 43.93 \u003d - 50.12 J / (mol * K) .

3. According to the tabular data, we find the thermal effect under standard conditions:

∆H 0 \u003d ∆H 0 arr C6H6 (g) - ∆H 0 arr C2H2 (g) \u003d 82.93 - 3 * 226.73 \u003d - 597.26 kJ / mol

4. Find the thermal effect at a given temperature:

∆H = ∆H 0 + ∆Ср (Т-Т 0) = - 597.26 * 10 3 + (-50.12) * (348- 298) = -599766 J / mol

b) Exact integration:

Let us consider the second, more complicated case, when the change in heat capacity depends on temperature, i.e. Ср=f(T), Cv=f(T).

Let us turn to the reaction equation in general form

dD + rR = qQ + pP

	a	b*10 3	c’*10 -5	C*10 6
D	+	+	-	+
R	+	+	+	-
Q	+	+	+	-
P	+	+	+	-

∆a=q*a(Q) + p*a(P) - ;

∆b=q*b(Q) + p*b(P) - ;

∆c’= q*c’(Q) + p*c’(P) - ;

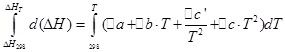
We will carry out the same operations for the isochoric process:

HEAT OF DISSOLUTION

The change in enthalpy during the transition of a solid, liquid or gaseous substance into a solution is called thermal or enthalpy of dissolution.

The heat of dissolution generally includes the heat of destruction of the crystal lattice (for solids), ionization and solvation.

To break the bond between the ions of a crystalline salt, energy is needed, i.e. while heat is absorbed. At the same time, ion hydration occurs in the aqueous solution; a bond is formed between the ions and molecules of H 2 O. The sign of the heat of dissolution is determined by the process that is energetically more pronounced.

LiBr: ∆H dist = - 49.02 kJ / mol - heat is released

KCl: ∆H dist = 7.23 kJ/mol - heat is absorbed

Distinguish: the integral heat of dissolution is the heat that is released or absorbed when 1 mole of a given substance is dissolved to form a solution of a given concentration. The integral heat of dissolution varies depending on the amount of the dissolved substance.

Distinguish: differential heat of dissolution - this is the heat that accompanies the dissolution of 1 mole of a given substance in infinitely large volume solution of this substance. Integral heats are widely used in calculating the heats of formation and heats of other reactions according to the Hess law. Differential heats of dissolution characterize the thermodynamic properties of solutions and the process of their formation.

LAB #8

DETERMINATION OF HEAT CAPACITY OF SOLID BODIES

Instruments and accessories: experimental setup FPT1-8.

Objective: determination of the heat capacity of metal samples by the calorimetric method using electrical heating.

Brief theory

Specific heat capacity of a substance - a value equal to the amount of heat required to heat 1 kg of a substance by 1 K:

Molar heat capacity - a value equal to the amount of heat required to heat 1 mol of a substance per 1 K:

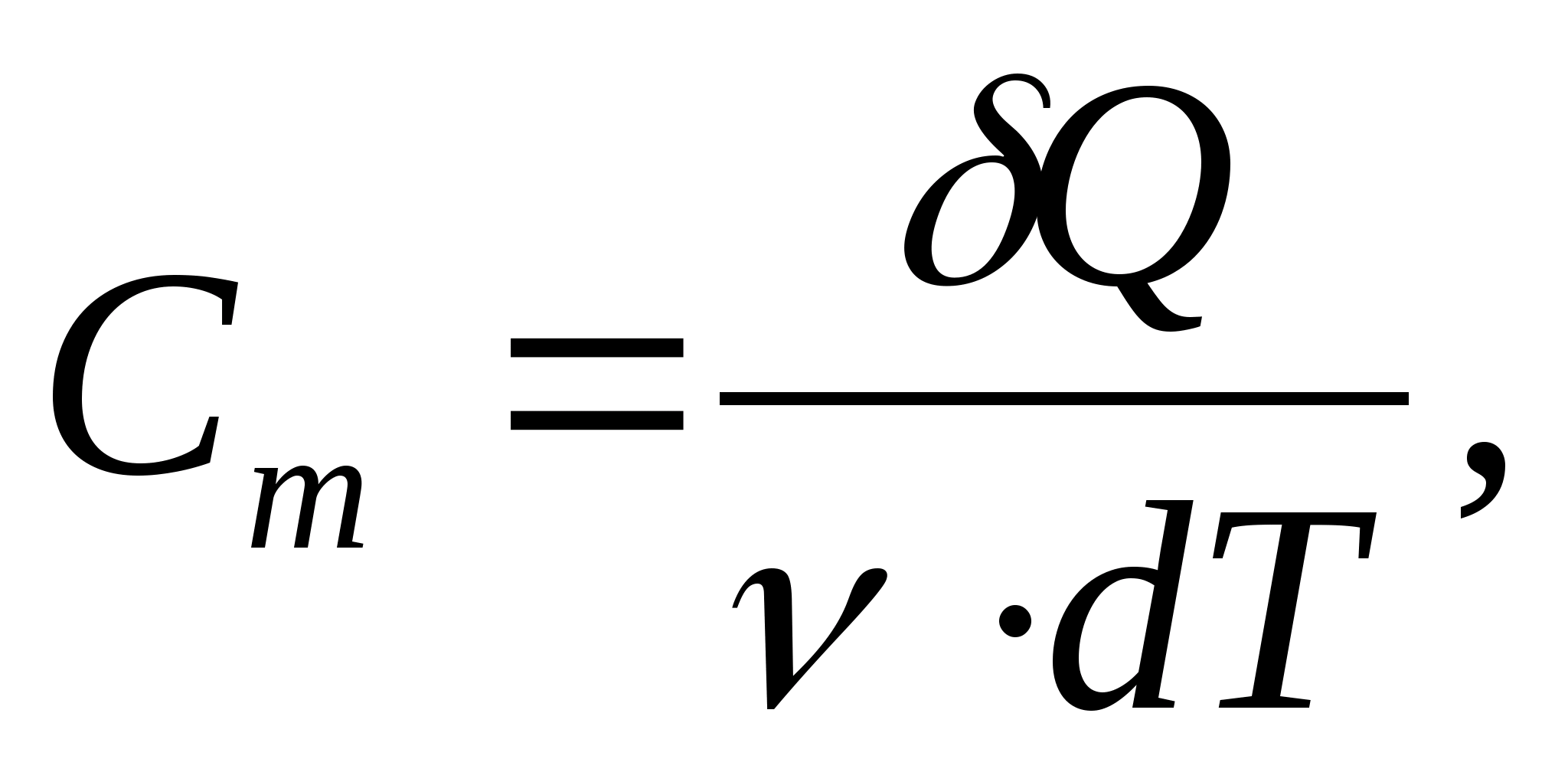
where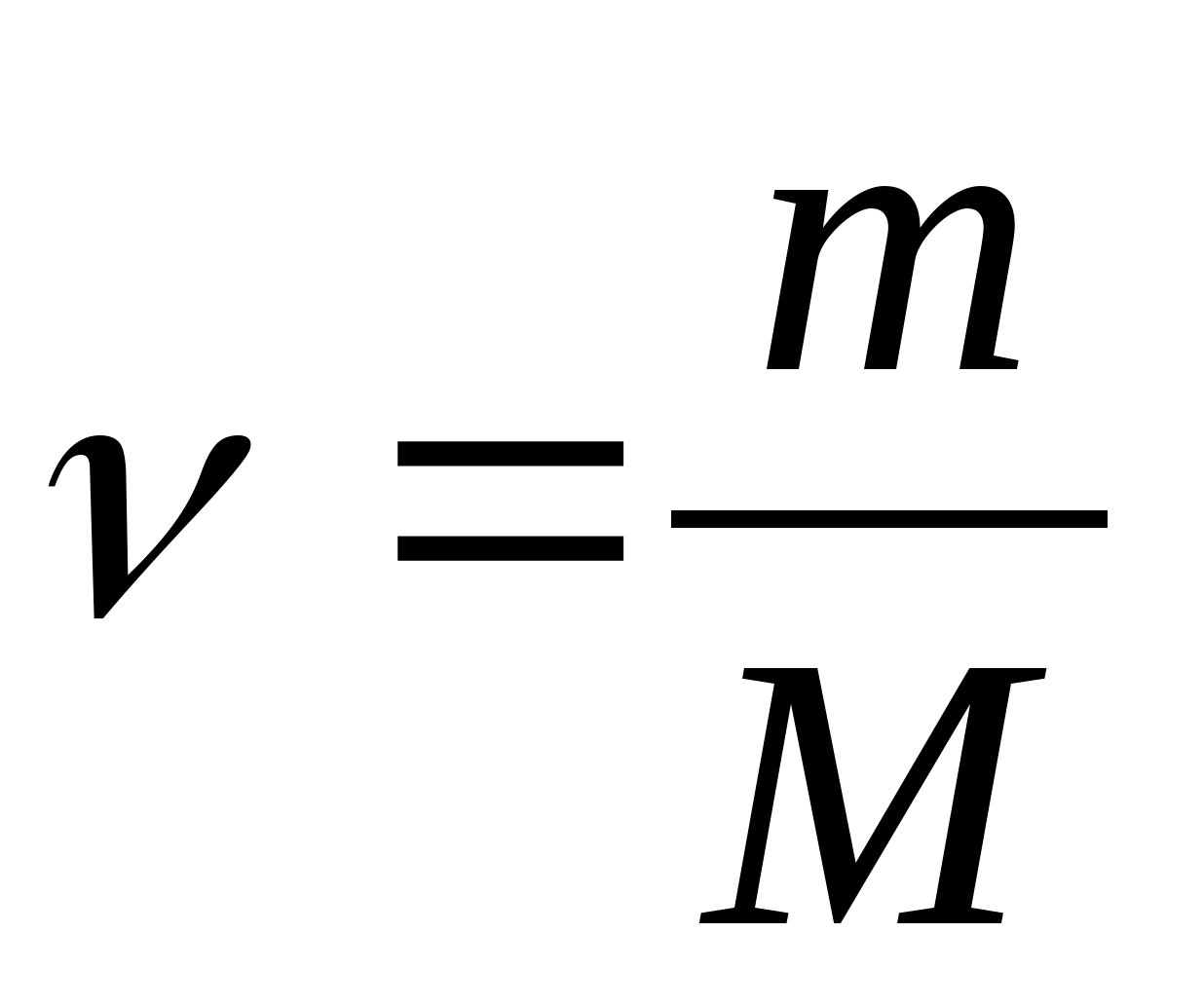

− amount of substance.

Specific heat c associated with molar C m ratio

where M is the molar mass of the substance.

Distinguish heat capacity at constant volume and constant pressure, if in the process of heating a substance its volume or pressure is maintained constant.

The smallest number of independent variables (coordinates) that completely determine the position of the system in space is called number of degrees of freedom .

According to Boltzmann's law on the uniform distribution of energy over the degrees of freedom of molecules, each translational and rotational degrees of freedom have an average kinetic energy equal to

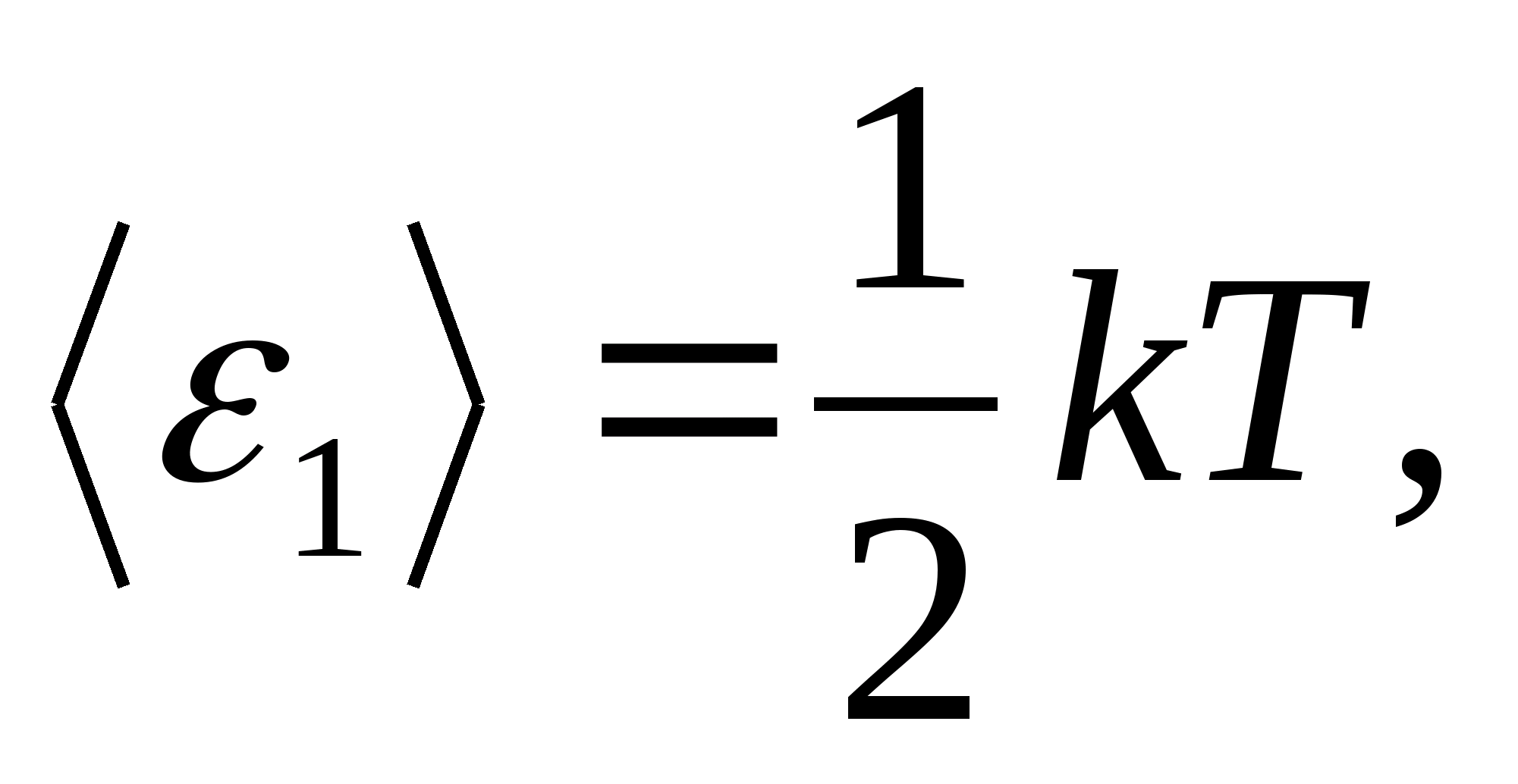
(where k is the Boltzmann constant), and for each vibrational degree of freedom, on average, the energy equal to

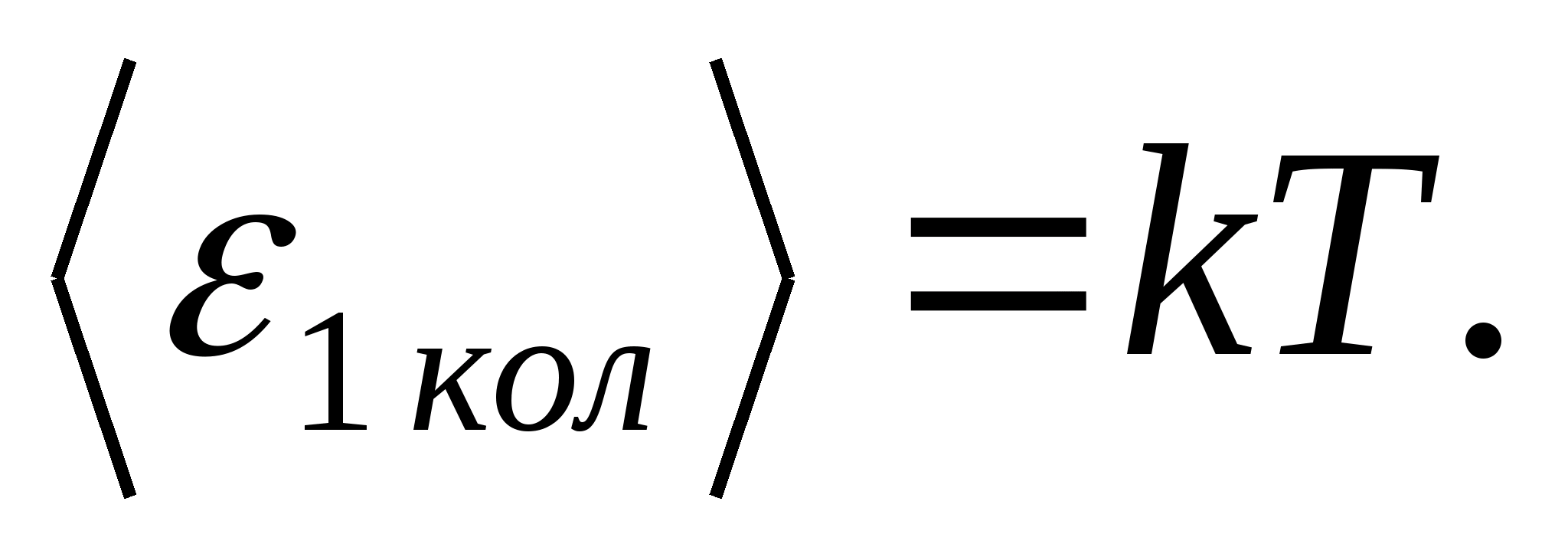
Thus, the average energy of a molecule

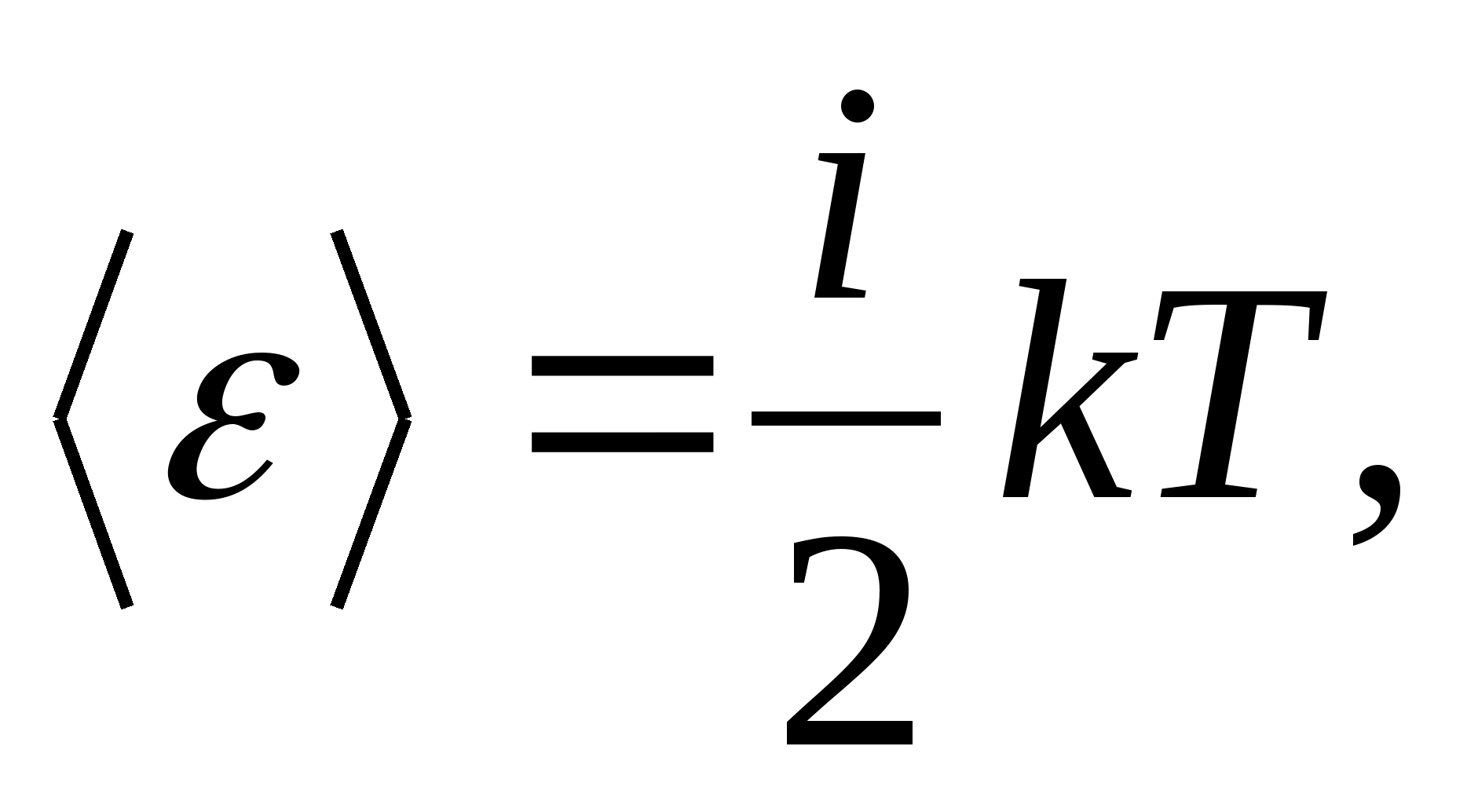
where i is the sum of the number of translational, the number of rotational and twice the number of vibrational degrees of freedom of the molecule:

For example, the average kinetic energy of monatomic ideal gas molecules (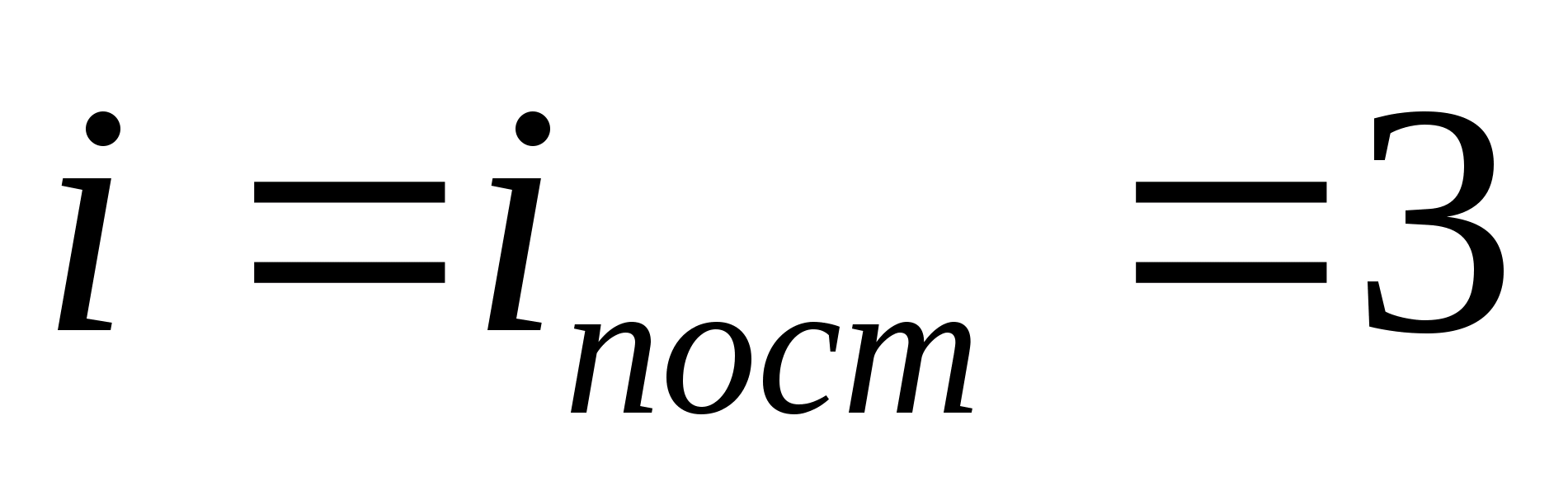

) is equal to

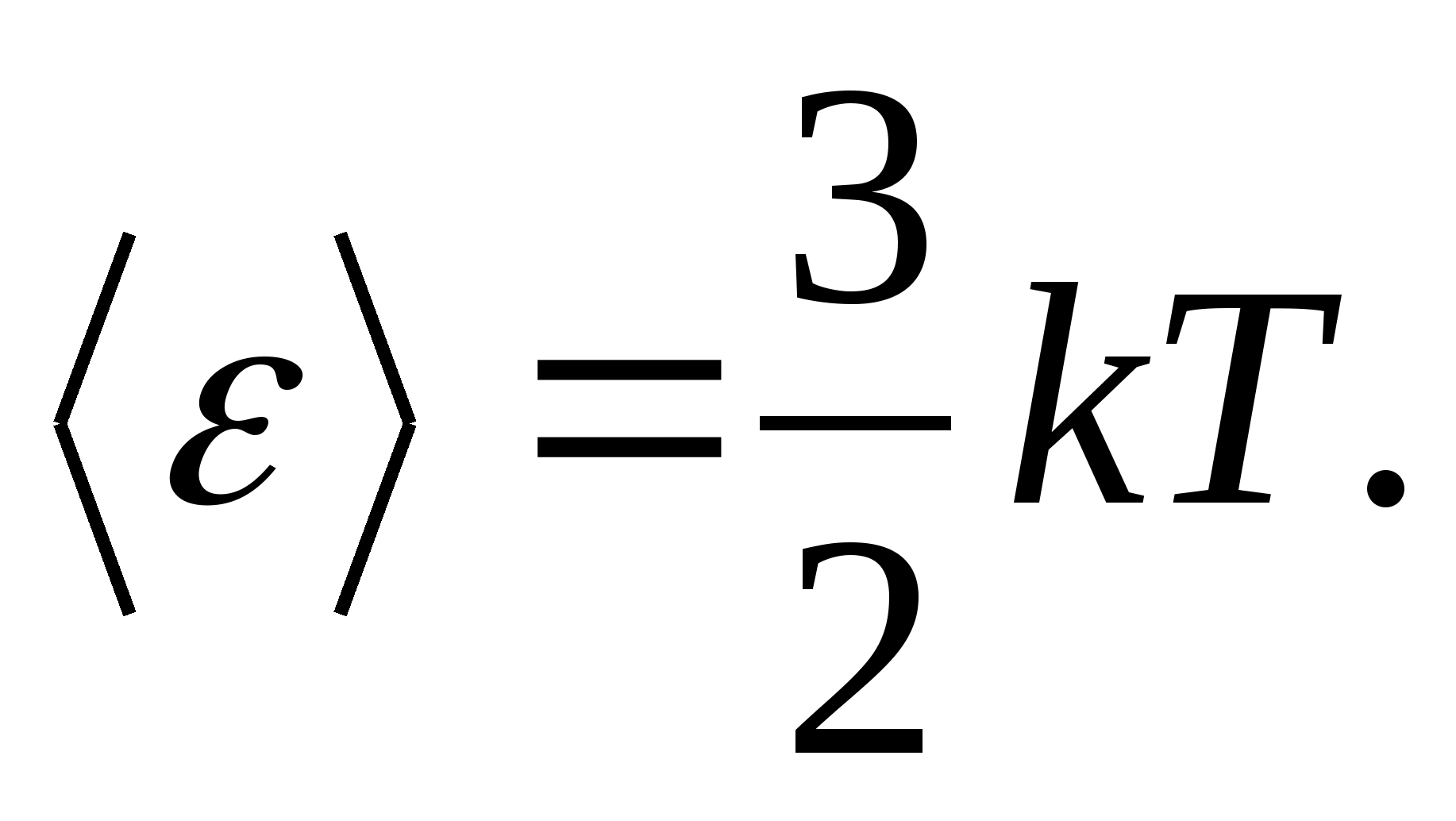
As models of a solid body, consider a correctly constructed crystal lattice, in the nodes of which particles (atoms, ions, molecules) are taken as material points, oscillate around their equilibrium positions - lattice nodes - in three mutually perpendicular directions. Thus, each particle constituting the crystal lattice is assigned three vibrational degrees of freedom, each of which, according to the law on the uniform distribution of energy over degrees of freedom, has the energy kT.

Then the average value of the total energy of the particle during oscillatory motion in the crystal lattice

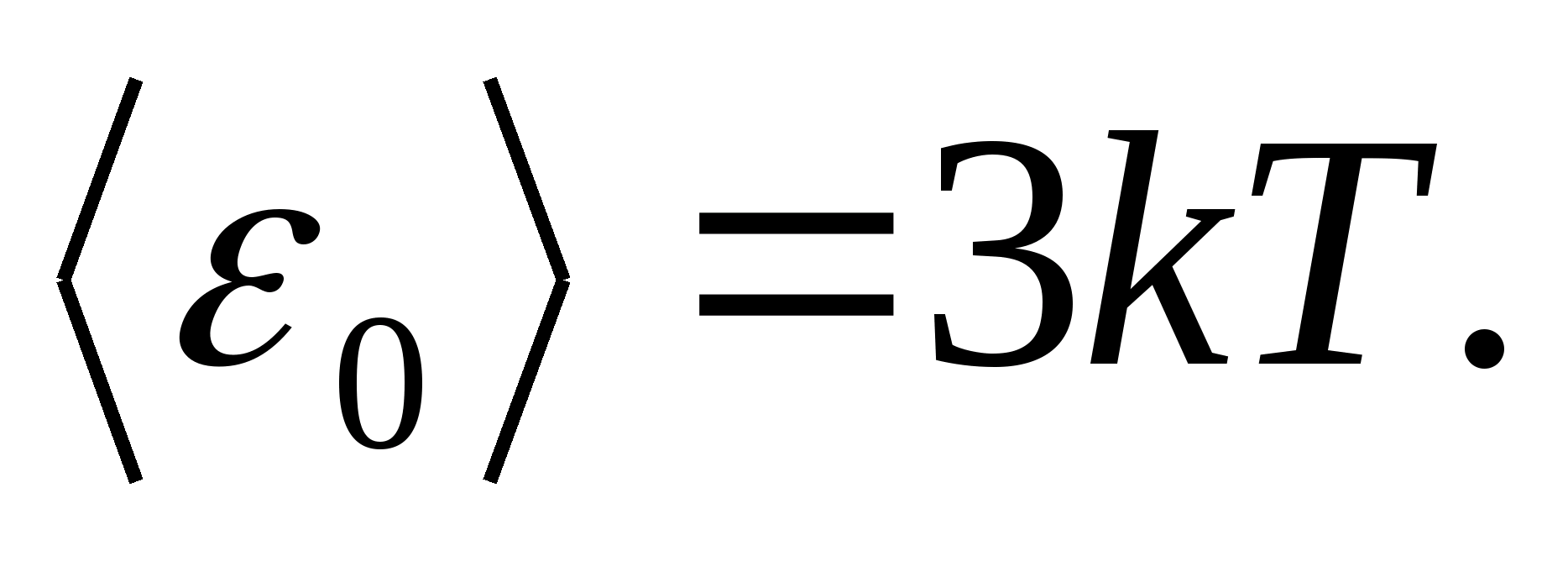
The total internal energy of one mole of a solid body is obtained by multiplying the average energy of one particle by the number of independently vibrating particles contained in one mole, i.e. to the Avogadro constant N A :

where R=N A  k is the universal (molar) gas constant, R= 8.31 J/(molK).

For solids, due to the small coefficient of thermal expansion, the heat capacities at constant pressure and constant volume practically do not differ. Therefore, taking into account (8.1), the molar heat capacity of a solid

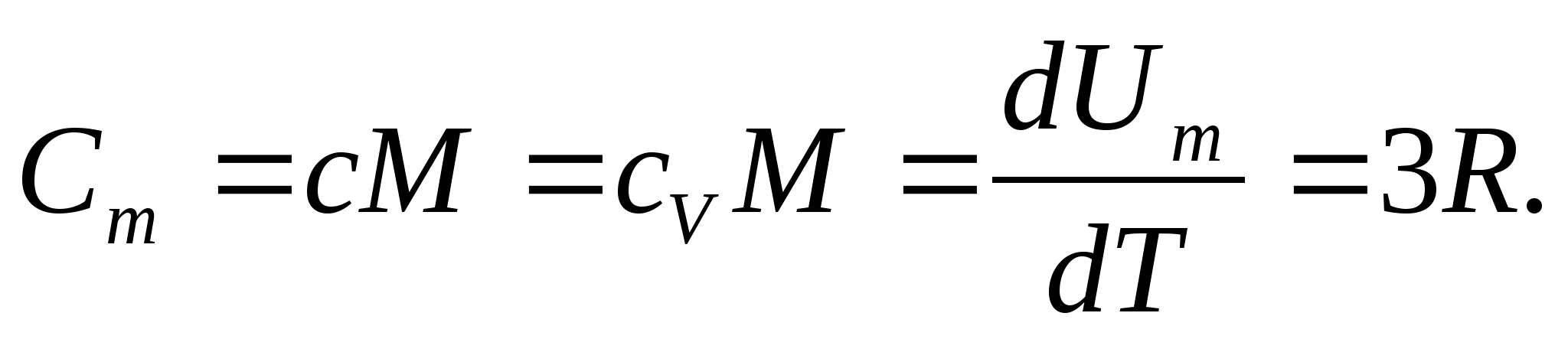(8.2)

Substituting the numerical value of the molar gas constant, we obtain:

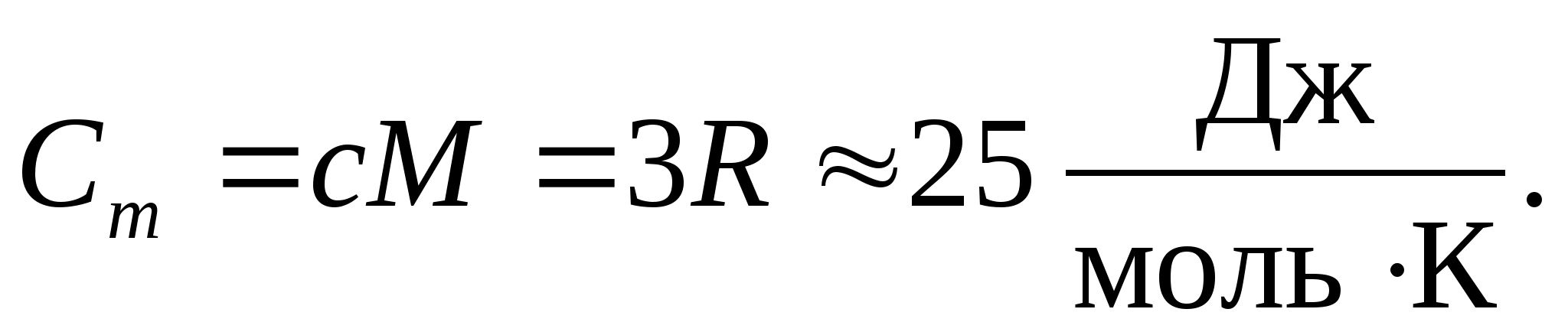
This equality holds to a fairly good approximation for many substances at room temperature and is called Dulong and Petit law : molar heat capacity of all chemically simple crystalline solids approximately equal to 25 J/(mol TO). As the temperature decreases, the heat capacities of all solids decrease, approaching zero at T0. Near absolute zero, the molar heat capacity of all bodies is proportional to T 3, and only at a sufficiently high temperature characteristic of each substance does equality (8.2) begin to hold. These features of the heat capacities of solids at low temperatures can be explained using the quantum theory of heat capacity created by Einstein and Debye.

To experimentally determine the heat capacity, the body under study is placed in a calorimeter, which is heated by an electric current. If the temperature of the calorimeter with the test sample is very slowly increased from the initial T 0 to  T, then the energy of the electric current will be used to heat the sample and the calorimeter:

where I and U− heater current and voltage;  − heating time; m 0 and m are the masses of the calorimeter and the test sample, With 0 and With− specific heat capacities of the calorimeter and test sample,  Q− heat loss to the thermal insulation of the calorimeter and to the surrounding space.

To exclude from equation (8.3) the amount of heat expended on heating the calorimeter and the loss of heat to the surrounding space, it is necessary, at the same heater power, to heat the empty calorimeter (without sample) from the initial temperature T 0 for the same temperature difference  T. The heat loss in both cases will be almost the same and very small, if the temperature of the protective casing of the calorimeter in both cases is constant and equal to room temperature:

Equations (8.3) and (8.4) imply

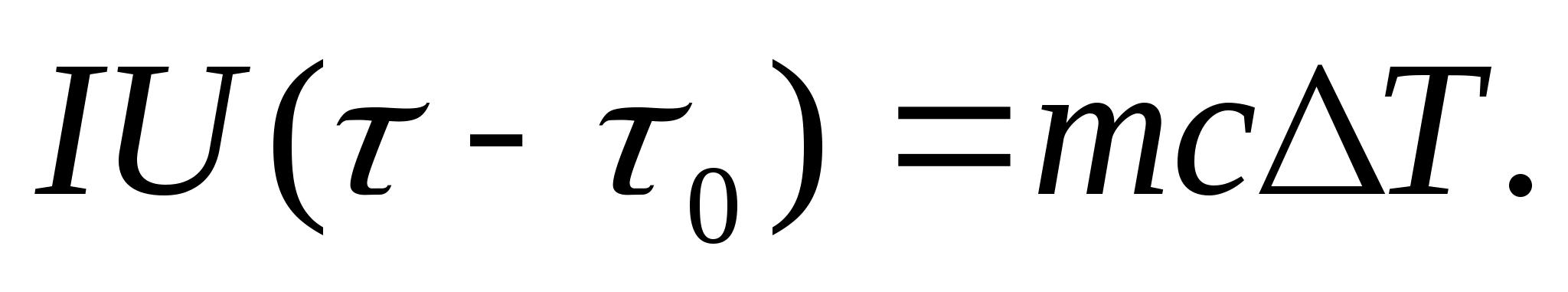(8.5)

Equation (8.5) can be used to experimentally determine the specific heat capacity of the material of the test sample. By changing the temperature of the calorimeter, it is necessary to plot the dependence of the difference in heating time on the change in temperature of the test sample: (  −  0)=f(T), according to the angular coefficient of which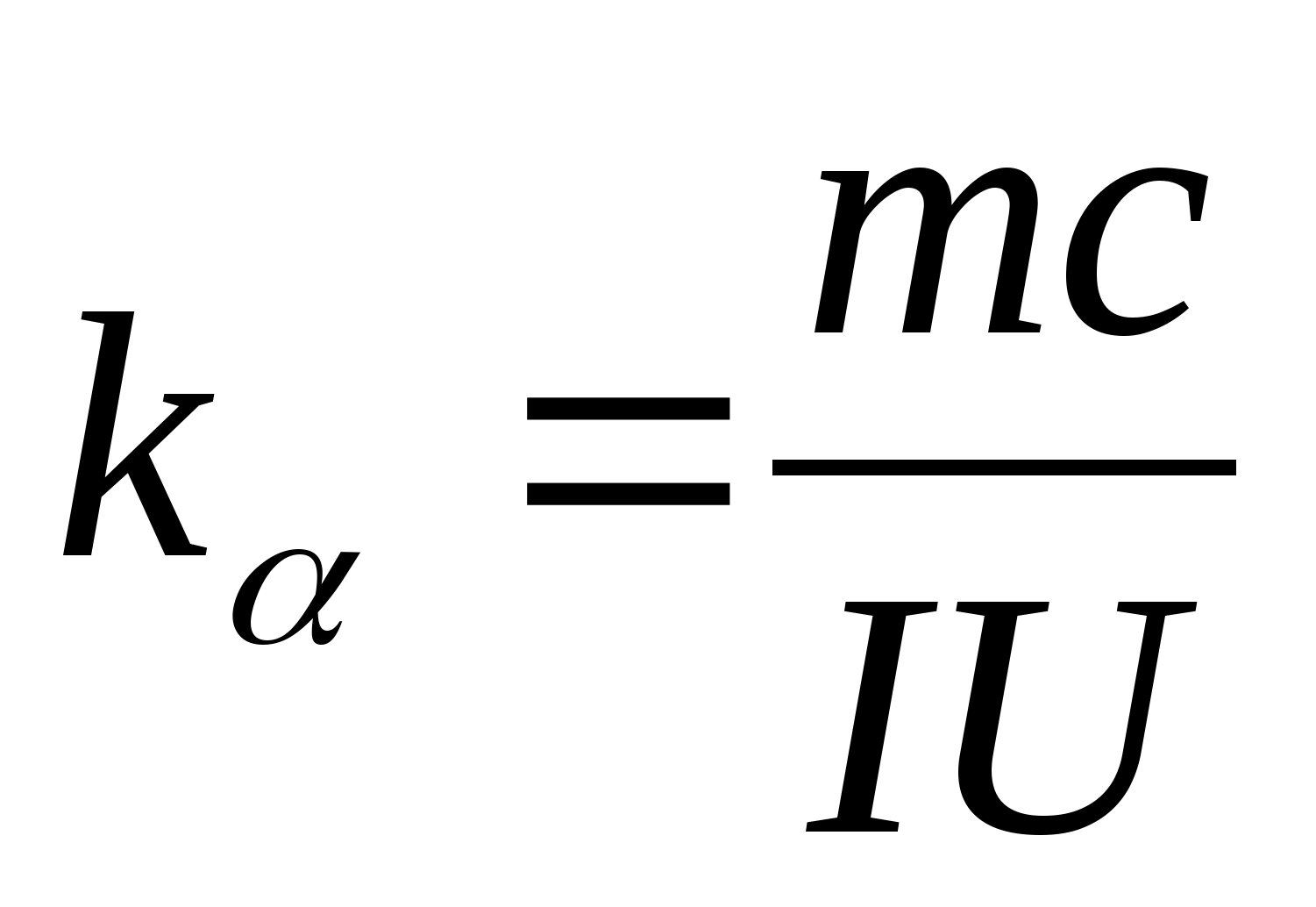

the specific heat capacity of the sample can be determined.

Description of the laboratory setup

To determine the heat capacity of solids, the FPT1-8 experimental setup is designed, the general view of which is shown in Fig. 8.1. The installation consists of three main parts: instrumental unit 1, operating element unit 2 and rack 3.

On the front panel of the control unit 1 there are: the “NETWORK” toggle switch, which connects the unit to the supply voltage network; toggle switch "HEATING", which turns on the heater; the “HEATING” regulator, with the help of which the heater power is regulated; voltmeter and ammeter, which measure the voltage and current in the heater circuit; stopwatch, which measures the heating time of the calorimeter. The stopwatch is activated when the instrument unit is powered on.

The block of the working element 2 is closed in front with a removable screen from org. glass. When performing work, the screen is hung on the back wall of the block of the working element. On the panel block of the working element is a digital thermometer 6 for measuring temperature. At the bottom, in the nests, there are 5 test samples made of various materials and a handle for placing the samples in the heater.

Heater 4 consists of a metal casing, heat-insulating material and a calorimeter.

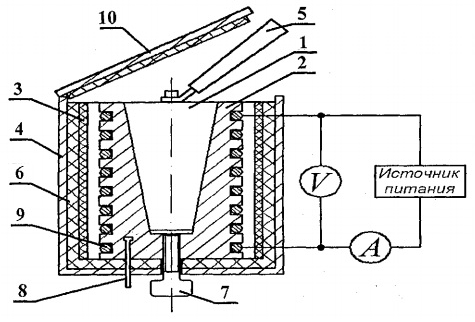
Samples are heated in a calorimeter, the scheme of which is shown in Fig. 8.2.

The calorimeter is a brass case 2 with a conical hole, where the test sample 1 is inserted. On the outer surface of the case, a heating coil 9 is placed in special grooves. Outside, the calorimeter case is thermally insulated with layers of asbestos 3 and glass fiber 6 and closed with an aluminum casing 4. The calorimeter is closed with a heat-insulating cover 10. After the end of the experiment, the sample can be pushed out of the conical hole of the calorimeter body with the help of screw 7. To remove the heated sample from the calorimeter and install the sample into the heater, handle 5 is used, located in a special socket next to the samples under study.

The temperature of the calorimeter is measured by a digital thermometer, the temperature sensor 8 of which is located in the housing 2 of the calorimeter.

Safety

When performing work, the general safety requirements in the mechanics laboratory are observed.

Work order

ATTENTION! The calorimeter takes a long time to cool down, so after measuring all the time values  0 heating of an empty calorimeter, immediately turn off the heating (see point 4 below). The maximum heating temperature for this unit is +44С.

1. Remove the transparent cover of the working element unit of the installation and hang it on the rear panel screws. Set the HEAT control knob to minimum. Turn on the installation with the "NETWORK" toggle switch.

2. Close the lid tightly on the empty calorimeter. Turn on the "HEAT" toggle switch. Using the HEAT regulator, set the voltage to 10-20 V (the higher the voltage, the faster the heating). Write in the table. 8.1 selected voltage values U and current I.

3. Starting from the temperature of the calorimeter t 0 specified by the teacher, after an interval of 1С enter in the table. 8.1 time values  0 corresponding to each reached temperature t.

4. Turn off the "HEAT" toggle switch, open the lid and cool the calorimeter to the initial temperature t 0 . To quickly cool the calorimeter, you can lower one of the samples into the calorimeter, except for the one indicated by the teacher (when installing the sample into the calorimeter, turn the screw at the bottom of the calorimeter to the left). The temperature will start to drop. When the cooling rate decreases, remove the heated sample and insert the next (cold) one, except for the one indicated by the teacher. To remove the sample, turn the screw at the bottom of the calorimeter to the right (clockwise), and then pull the sample out with the handle.

Table 8.1

				T= t− t 0 ,					 =  −  0 ,	J/(kgK)	C m =WithM, J/(molK)

5. Turning the screw to the left, place one of the test samples, taken as instructed by the teacher, into the calorimeter. Close the lid of the calorimeter tightly and wait 2-3 minutes for the calorimeter and sample temperatures to equalize.

6. Turn on the "HEAT" toggle switch and set the same voltage in the circuit as when heating the empty calorimeter.

7. Starting from the same initial calorimeter temperature t 0, after an interval of 1С enter in the table. 8.1 time values  corresponding to each reached temperature t.

8. Set the “HEATING” regulator to the extreme left position (to the minimum), turn off the “HEATING” toggle switch, open the lid of the calorimeter. To remove the sample from the calorimeter, turn the screw to the right, then remove the heated sample using the handle.

9. Turn off the unit with the "NETWORK" toggle switch.

10. Translate all the values ​​of the quantities  0 and  into values ​​in seconds (without minutes) and enter them in the table. 8.1. For each line of the table. 8.1 calculate the values ​​of   =  −  0 and  T= t− t 0 .

11. Make an estimated calculation of the specific heat capacity of the sample using the formula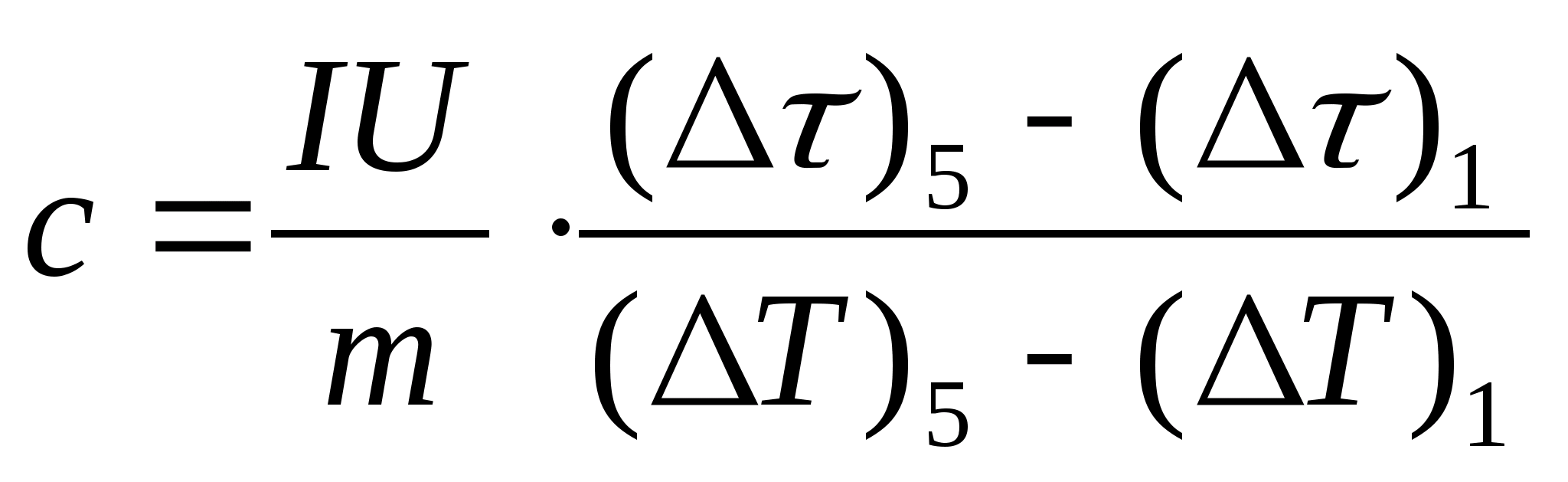

, where the mass of the sample m=139.5 g (brass) or m=129.7 g (steel) or m=46.05 g (duralumin). Come to the teacher for verification.

Processing measurement results

1. Plot   =f(T) the dependence of the difference in the heating time of the calorimeter with the sample and the empty calorimeter on the temperature change of the calorimeter, select any two points on the graph and determine the slope of the straight line using the formula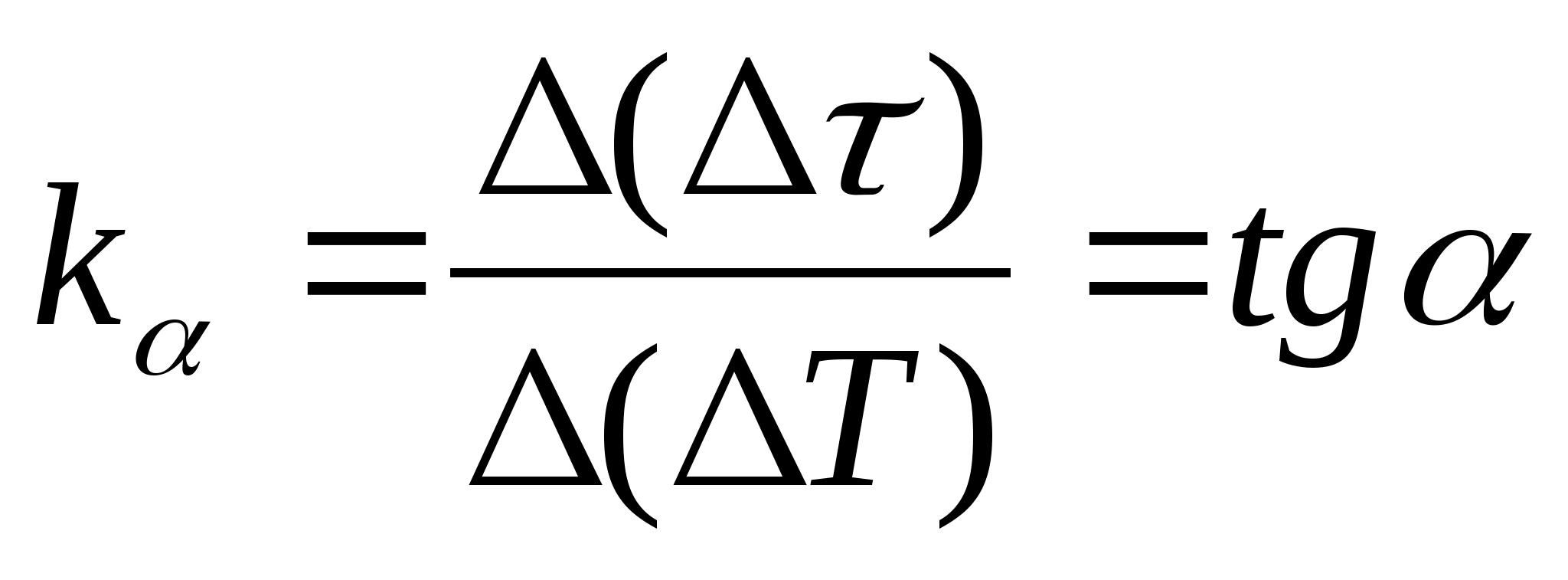

, where  − the angle of inclination of the graph to the axis  T (if the units of   and  T are shown on both axes as segments of the same length).

2. Using the value of the slope k  , determine the specific heat capacity of the sample using the formula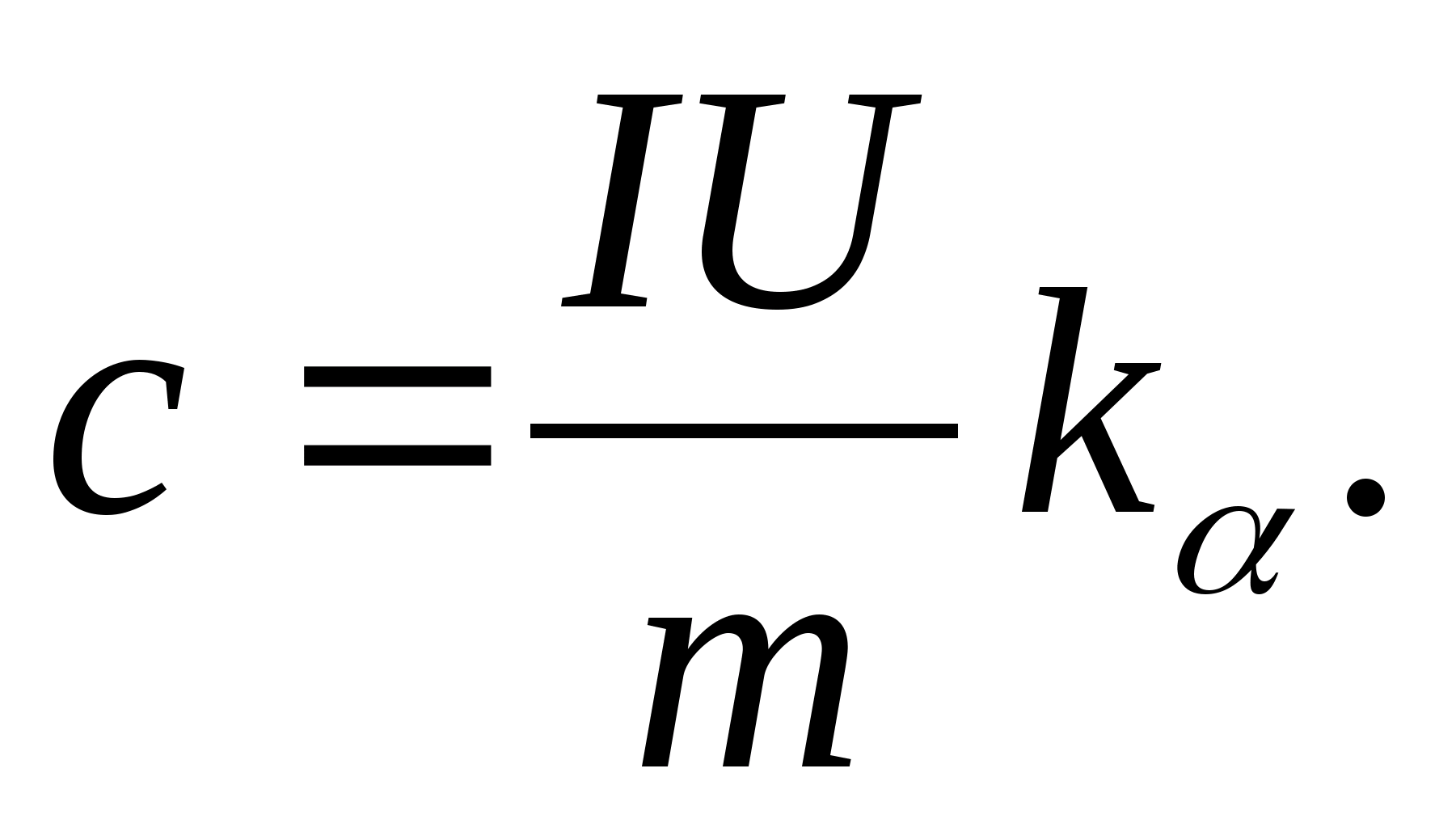

3. Using the data in table 8.2 (or the periodic table), determine the molar heat capacity of the sample using the formula C m =WithM.

Table 8.2

	Sample material	Atomic mass, kg/mol

As a model of a solid body, let us consider a correctly constructed crystal lattice, in the nodes of which particles (atoms, ions, molecules), taken as material points, oscillate around their equilibrium positions - lattice nodes - in three mutually perpendicular directions. Thus, each particle constituting the crystal lattice is assigned three vibrational degrees of freedom, each of which, according to the law of equipartition of energy over degrees of freedom (see § 50), has the energy kT.

Internal energy of a mole of a solid body

U m \u003d 3N A kT \u003d 3RT,

where N A is Avogadro's constant; N A k= R (R is the molar gas constant).

Molar heat capacity of a solid

i.e. molar (atomic) heat capacity chemically simple bodies in the crystalline state is the same (equal to 3 R) and does not depend on temperature. This law was empirically obtained by the French scientists P. Dulong (1785-1838) and L. Petit (1791-1820) and is titleDulong and Petit law.

If the solid is a chemical compound (for example, NaCl), then the number of particles in the mole is not equal to the Avogadro constant, but is equal to nN A , where n - number of atoms in a molecule (for NaCl, the number of particles in a mole is 2 N and, so, one mole of NaCl contains N A Na atoms and N A Cl atoms). So the molar heat capacity solid chemical compounds

C V \u003d 3R25n J / (mol K),

i.e., equal to the sum of the atomic heat capacities of the elements that make up this compound.

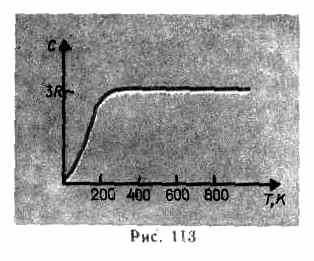
As experimental data show (Table 4), for many substances the Dulong and Petit law is satisfied with a fairly good approximation, although some substances (C, Be, B) have significant deviations from the calculated heat capacities. In addition, as in the case of gases (see § 53), experiments on measuring the heat capacity of solids at low temperatures have shown that it depends on temperature (Fig. 113). Near zero Kelvin, the heat capacity of bodies is proportional to T 3 , and only at sufficiently high temperatures, characteristic of each substance, condition (73.1) is satisfied. Diamond, for example, has a heat capacity of 3 R at 1800 K! However, for most solids, room temperature is already high enough.

The discrepancy between the experimental and theoretical values ​​of the heat capacities calculated on

the basis of classical theory, explained, based on the quantum theory of heat capacities, A. Einstein and P. Debye (1884-1966).

§ 74. Evaporation, sublimation, melting and crystallization. Amorphous bodies

In both liquids and solids, there is always a certain number of molecules whose energy is sufficient to overcome attraction to other molecules and which are able to break away from the surface of a liquid or solid and pass into the space surrounding them. This process for liquid is called evaporation(or vaporization), for solids - sublimation(or sublimation).

Evaporation of liquids occurs at any temperature, but its intensity increases with increasing temperature. Along with the evaporation process, a compensating process takes place condensation vapor to liquid. If the number of molecules leaving the liquid per unit of time through a unit surface is equal to the number of molecules passing from vapor to liquid, then dynamic balance between evaporation and condensation processes. A vapor in equilibrium with its liquid is called rich(see also § 62).

For most solids, the sublimation process at ordinary temperatures is negligible and the vapor pressure over the surface of the solid is low; it increases with increasing temperature. Intensively sublimate substances such as naphthalene, camphor, which is detected by a sharp, characteristic smell. Sublimation occurs especially intensively in a vacuum - this is used to make mirrors. A well-known example of sublimation is the transformation of ice into steam - wet laundry dries out in the cold.

If a solid body is heated, then it internal energy(the sum of the energy of vibrations of particles at the lattice sites and the energy of interaction of these particles) increases. As the temperature rises, the amplitude of particle oscillations

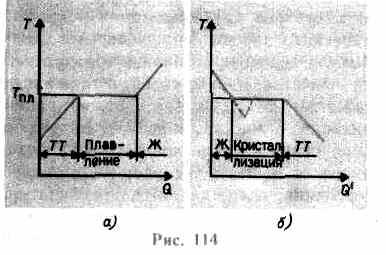
increases until the crystal lattice collapses - the solid melts. On fig. 114 a an approximate dependence is shown T(Q), where Q- the amount of heat received by the body during melting. As the message to the solid warmth body its temperature rises, and at the melting point T pl begins the transition of the body from a solid to a liquid state. Temperature T pl remains constant until the entire crystal is melted, and only then the temperature of the liquid begins to rise again.

Heating a solid up to T pl does not yet convert it into a liquid state, since the energy of the particles of the substance must be sufficient to destroy the crystal lattice. In the process of melting, the heat imparted to the substance is used to perform work on the destruction of the crystal lattice, and therefore T pl =const until the entire crystal is melted. Then the heat supplied will go again to increase the energy of the particles of the liquid and its temperature will begin to rise. The amount of heat required to melt 1 kg of a substance is called specific heat of fusion.

If the liquid is cooled, then the process proceeds in the opposite direction (Fig. 114, b; Q" - the amount of heat given off by the body during crystallization): first, the temperature of the liquid decreases, then at a constant temperature equal to T pl, begins crystallization, after its completion, the temperature of the crystal begins to decrease. For the crystallization of a substance, the presence of so-called crystallization centers - crystalline nuclei, which can be not only crystals of the formed substance, but also impurities, as well as dust, soot, etc. The absence of crystallization centers in a pure liquid makes it difficult for the formation of microscopic crystals, and the substance, remaining in a liquid state, cools to a temperature lower than crystallization temperature, thus forming supercooled liquid(on 114, b it corresponds to the dashed curve). With strong supercooling, spontaneous formation of crystallization centers begins and the substance crystallizes rather quickly.

Usually, supercooling of the melt occurs from fractions to tens of degrees, but for a number of substances it can reach hundreds of degrees. Due to the high viscosity, highly supercooled liquids lose their fluidity, retaining their shape, like solids. These bodies are called amorphous solids; these include resins, wax, sealing wax, glass. Amorphous bodies, being thus supercooled liquids, isotropic, i.e., their properties are the same in all directions; for them, as well as for liquids, it is characteristic short range order in the arrangement of particles; in them, in contrast to liquids, the mobility of particles is rather small. A feature of amorphous bodies is that they do not have a specific melting point, that is, it is impossible to indicate a specific temperature above which a liquid state could be ascertained, and below a solid state. From experience it is known that in amorphous bodies the process of crystallization can be observed over time, for example, crystals appear in glass; it, losing transparency, begins to become cloudy and turn into a polycrystalline body.

Recently, widespread use in national economy got polymers- organic amorphous bodies, the molecules of which consist of a large number of identical long molecular chains connected by chemical (valence) bonds. Polymers include both natural (starch, protein, rubber, fiber, etc.) and artificial (plastic, rubber, polystyrene, lavsan, nylon, etc.) organic substances. Polymers are inherent strength and elasticity; some polymers withstand stretching 5-10 times their original length. This is explained by the fact that long molecular chains can, under deformation, either fold into dense balls or stretch into straight lines. The elasticity of polymers manifests itself only in a certain temperature range, below which they become hard and brittle, and above - plastic. Although a lot of synthetic polymeric materials have been created (artificial fibers, leather substitutes, building materials, metal substitutes, etc.), the theory of polymers has not yet been fully developed. Its development is determined by the demands of modern technology, which requires the synthesis of polymers with predetermined properties.

The specific heat capacity of a substance is understood as the value
, (1)
where is the amount of heat imparted to the body.
is the change in temperature that occurs in
as a result of the transfer of heat to the body,
m is the mass of the heated body.
Experience usually determines the average specific heat substance c, numerically equal to the amount of heat that must be imparted to a unit mass of this substance in order to raise its temperature by:
(2),
where is the difference between the final and initial temperatures of the body under study.
Various calorimetric methods are used to experimentally determine the heat capacity. The variety of these methods is due to the fact that accurate measurement of the amount of heat imparted to the body requires the elimination of heat losses that are not taken into account when heating the body under study.
Usually, in the so-called calorimeters with an isothermal shell, a calculated or experimentally determined correction for radiation is introduced, that is, the amount of heat that the calorimeter receives or gives off to the external environment by radiation during the experiment.
However, it is possible to significantly reduce heat losses by introducing good thermal insulation or by reducing the duration of the experiment, which is achieved by a high heating rate of the sample ~ (pulse method for measuring heat capacity), at which heat losses will be small compared to the total amount of heat supplied.
One of the most accurate methods for determining heat capacity is the adiabatic calorimeter method. Difficulties associated with the need to take into account heat losses in calorimeters of this type are eliminated by the fact that measurements are made under conditions of thermal equilibrium, that is, under conditions of equal temperatures of the sample under study and the block surrounding the sample. The advantages of this method, along with high accuracy, also include the possibility of determining the heat capacity of solids in a wide temperature range, which is especially important if substances undergo phase transformations.
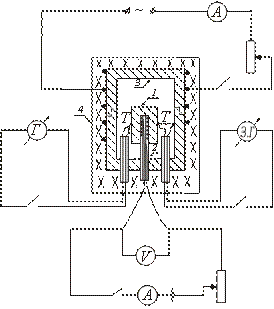
The device of one of the types of adiabatic calorimeter is shown schematically in the figure. The test sample 1 is placed in the copper block 3 and together with it is heated in furnace 4. Heater 2 is introduced inside the sample, which allows additional heating of the sample.
After turning on furnace 4, in which the block with the sample is placed, the temperature of the sample begins to rise, remaining below the temperature of the block. To establish equality between the temperatures of the sample and the block, turn on the heater placed inside the sample. When the sample temperature is slightly above the block temperature, the internal heater is turned off.
Subsequently, this heater is turned on and off periodically, so that the temperature difference between the sample and the block changes sign all the time.
At the moment when it is equal to zero (when the internal heater is on), there is no heat exchange between the sample and the block, and the entire amount of heat released by the internal heater is spent only on heating the sample; specific heat in this case can be determined by formula (2).
The amount of heat released by the internal heater is determined by the formula:

where I is the current of the internal heater;
V is the voltage drop across it;
- the time interval during which the temperature increased by .
Then
(4)

where is the time during which the temperature of the sample changed by .
In differential form, formula (4) has the form
(5)
The temperature of the sample is measured with a T thermocouple. The temperature difference between the block and the sample is measured with a differential thermocouple. To determine the sample temperature, a thermocouple calibration curve T is used. The temperature difference between the block and the sample is determined in divisions of the galvanometer scale (since it is only necessary to fix the moment when the temperature difference between the block and the sample changes sign).
Completing of the work.
The sample is put on a heater placed inside a copper block. The thermocouple junctions T and are connected to the sample and the block. The oven is closed with a lid. The electric winding of the furnace, in which the block is placed, is switched on. The heater placed inside the sample is periodically turned on and off, and the values ​​of I and V are recorded in the circuit of the internal heater.

Before starting measurements, it is necessary to check the zero position of the mirror galvanometer. To do this, by disconnecting the thermocouple from the galvanometer, they expect the bunny to stop fluctuating along the scale. If after this the image of the thread does not coincide with zero, then by moving the scale this coincidence is achieved.
Dependence curves of T and on time are plotted.
From the slope of the curve T(t) at the point where it changes sign (that is, when thermal equilibrium is established), the specific heat is calculated using formula (5). This heat capacity refers to the temperature to be read off the curve T(t) at the moment when the temperature difference between the block and the sample changes sign.